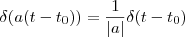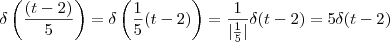Estou com um pouco de dúvidas quanto a calcular a integral:
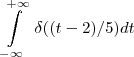
De forma generalizada, integrando o impulso(ou a distribuição Delta de Dirac) de
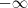 até
até 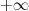 obtenho a função degrau unitário(função de Heaviside):
obtenho a função degrau unitário(função de Heaviside):De forma geral:
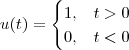
Neste caso, a função está temporalmente deslocada em (t-2).
Usei o wolframalpha para ver o resultado, mas não entendi o porque do resultado ser igual a 5.
Como o divisor do argumento de
 "passou" como produto?
"passou" como produto?Muito obrigado!