 por renan_a » Qua Jan 09, 2013 17:57
por renan_a » Qua Jan 09, 2013 17:57

Galera, estou com sérias dificuldades com integrais por frações parciais, entretanto, as mais simples estou conseguindo fazer.
No entando, esta integral não estou conseguindo resolver.
se fosse x^2 no numerador, eu poderia fazer com A +(Bx+C) por que daria o grau, correto?
mas não sei como faço com essa...
Aproveitando o tópico, alguém me indica algum livro ou pdf que trate bem desse tópico em questão?
Abraços a todos.
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Qua Jan 09, 2013 20:16
por young_jedi » Qua Jan 09, 2013 20:16
separe da seguinte forma
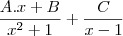
dai teremos
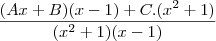


igualando as expressões teremos o sistema

resolvendo temos

tente concluir
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por renan_a » Qua Jan 09, 2013 22:05
por renan_a » Qua Jan 09, 2013 22:05
Pô, meu velho... Sem palavras pra te agradecer, deu certinho. Depois do resultado das incógnitas, tudo saiu nos ''conformes''. Abraço
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integral racional]
por brunaoliveira » Dom Mai 26, 2013 21:07
- 0 Respostas
- 1015 Exibições
- Última mensagem por brunaoliveira

Dom Mai 26, 2013 21:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral Racional
por Fernandobertolaccini » Seg Jul 21, 2014 19:40
- 0 Respostas
- 892 Exibições
- Última mensagem por Fernandobertolaccini

Seg Jul 21, 2014 19:40
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de fração racional] Deduza uma formiula para:
por Job1992 » Ter Nov 26, 2013 22:29
- 1 Respostas
- 1764 Exibições
- Última mensagem por e8group

Sáb Nov 30, 2013 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Contradominio de função racional
por joaofonseca » Dom Jul 03, 2011 11:54
- 9 Respostas
- 33347 Exibições
- Última mensagem por LuizAquino

Sex Fev 10, 2012 10:52
Funções
-
- Calculo de Limite de Função Racional
por joaofonseca » Qua Mai 04, 2011 20:50
- 3 Respostas
- 2360 Exibições
- Última mensagem por LuizAquino

Qua Mai 04, 2011 23:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



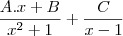
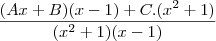






 .
.



