por iarapassos » Qui Jan 03, 2013 18:52
por iarapassos » Qui Jan 03, 2013 18:52
A questão é o seguinte:
Calcule a área plana limitada pelas funções:
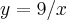
,
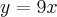
e

.
Achei que seria o seguinte:
Como sabemos, através do estudo deste assunto. Temos que a região será a integral de f(x)-g(x), sendo f(x)>=g(x).
Bem, também sabemos que essa area deve ser subdivida em duas areas menores. A Area total será a soma de S1 e S2.
A minha dúvida é: Eu tenho três funções. Neste caso, a area entre elas será a maior menos as outras? Ou eu subtraio apenas uma?
Me ajudem , please!
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Russman » Qui Jan 03, 2013 20:16
por Russman » Qui Jan 03, 2013 20:16
E acredito que a área a ser calculada é a em forma triangular, bem do centro do gráfico.

- Grafico
- ScreenHunter_02 Jan. 03 20.31.gif (3.88 KiB) Exibido 2655 vezes
Se sim, então você deve ir subtraindo e adicionando áreas menores de forma a varrer somente a de interesse. Os vértices da área são respectivamente

,

e

.
Eu adicionaria a área de

até

do gráfico de
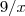
, subtrairia a parte de baixo que é a área do gráfico de

de

até

, completaria com a área de
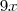
de

até

e por fim descontaria o que resta , que é a area de

de

até

.
Acredito que assim conseguimos varrer a área que foi limitada pelas 3 funções. A sua integral é
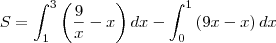
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58
- 1 Respostas
- 1935 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
-
- Como encontrar a área limitada por duas funções?
 por VenomForm » Qua Fev 27, 2013 15:09
por VenomForm » Qua Fev 27, 2013 15:09
- 2 Respostas
- 2891 Exibições
- Última mensagem por Russman

Qua Fev 27, 2013 19:14
Cálculo: Limites, Derivadas e Integrais
-
- região R limitada
 por Ana Maria da Silva » Qui Out 31, 2013 11:14
por Ana Maria da Silva » Qui Out 31, 2013 11:14
- 2 Respostas
- 1990 Exibições
- Última mensagem por Ana Maria da Silva

Seg Nov 04, 2013 20:54
Cálculo: Limites, Derivadas e Integrais
-
- AREA LIMITADA
 por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
por ELCIO GOMES DE SOUZA » Dom Ago 24, 2008 16:55
- 3 Respostas
- 7146 Exibições
- Última mensagem por admin

Ter Ago 26, 2008 19:02
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02
- 0 Respostas
- 1128 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
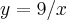 ,
, 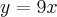 e
e  .
.

 ,
,  e
e  .
.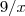 , subtrairia a parte de baixo que é a área do gráfico de
, subtrairia a parte de baixo que é a área do gráfico de  de
de 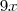 de
de