Estou estudando sequências e séries, e acabei precisando resolver esse limite:

Sei que
 é uma indeterminação.
é uma indeterminação.Então fiz essa resolução:
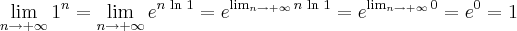
Está correta?
Usei um programa matemático (Sage), e a resposta para o limite realmente foi 1.
Desde já agradeço!


 é uma indeterminação.
é uma indeterminação.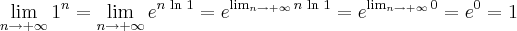

 definida por
definida por  .É fácil ver que para quaisquer valor que
.É fácil ver que para quaisquer valor que  assmuir ,
assmuir , 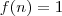 . Sendo assim, tomar o limite quando
. Sendo assim, tomar o limite quando 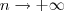 de
de 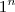 é o mesmo que o de
é o mesmo que o de  .Logo ,
.Logo , 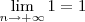 . Não vejo erro na sua solução , mas acredito que é desnecessário todo este procedimento .
. Não vejo erro na sua solução , mas acredito que é desnecessário todo este procedimento .
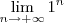 como
como 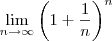 . Algumas pessoas pensam que este limite é um pois "aplicam" o limite "dentro" e depois aplicam "fora", fazendo
. Algumas pessoas pensam que este limite é um pois "aplicam" o limite "dentro" e depois aplicam "fora", fazendo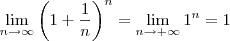 .
. e
e  variam simultaneamente, e você deve levar isto em conta.
variam simultaneamente, e você deve levar isto em conta.

Fabio Wanderley escreveu:Bom dia, pessoal,
Estou estudando sequências e séries, e acabei precisando resolver esse limite:
Sei queé uma indeterminação.
Então fiz essa resolução:
Está correta?
Usei um programa matemático (Sage), e a resposta para o limite realmente foi 1.
Desde já agradeço!
 é uma indeterminação", o que queremos dizer formalmente é: se
é uma indeterminação", o que queremos dizer formalmente é: se  e
e 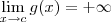 (ou
(ou  ), então
), então  é uma indeterminação.
é uma indeterminação. . Portanto, temos simplesmente que:
. Portanto, temos simplesmente que:
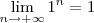
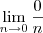
 e
e  , então
, então  é uma indeterminação.
é uma indeterminação. . Como nesse limite temos que n não é zero (ele apenas se aproxima de zero), podemos simplesmente escrever:
. Como nesse limite temos que n não é zero (ele apenas se aproxima de zero), podemos simplesmente escrever:


santhiago escreveu:Não vejo erro na sua solução , mas acredito que é desnecessário todo este procedimento .
MarceloFantini escreveu:(...)
As duas quantidades,e
variam simultaneamente, e você deve levar isto em conta.
LuizAquino escreveu:(...)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.