 por Sherminator » Qua Nov 28, 2012 07:33
por Sherminator » Qua Nov 28, 2012 07:33
Bom dia.
Estou aqui com um problema que não consigo resolver, preciso de determinar o parâmetro k, de forma a que a função g, seja contínua em todo o seu domínio, alguém me ajuda se faz favor?

-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por Russman » Qua Nov 28, 2012 14:11
por Russman » Qua Nov 28, 2012 14:11
Para que a função seja contínua é necessário, nesse caso, que tenha o mesmo valor para

.
Aplique

na equação para

e

na equação para
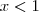
. Em seguida iguale as duas e isole o valor

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Sherminator » Qua Nov 28, 2012 15:06
por Sherminator » Qua Nov 28, 2012 15:06
Sendo assim ficaria:
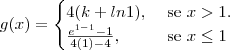

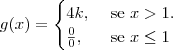
Será que resolvi bem até aqui? A de baixo é uma indeterminação, verdade? Sendo assim terei de resolver a sua indeterminação? O meu problema é mesmo trabalhar com o

, faz-me bastante confusão.
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por Sherminator » Qui Nov 29, 2012 14:00
por Sherminator » Qui Nov 29, 2012 14:00
Alguém me poderia dizer se o meu procedimento foi correto e ajudar-me a partir daí se faz favor?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por Fabio Wanderley » Qui Nov 29, 2012 14:08
por Fabio Wanderley » Qui Nov 29, 2012 14:08
Olá, Sherminator,
Se você tiver acesso ao livro do Guidorizzi (vol. 1, 5 ed.), observando as páginas 134 e 135, imagino que você conseguirá resolver a função para

.
Agora estou de saída. Logo que puder eu tentarei ajudá-lo, caso ninguém tenha o feito.
Até mais!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por Fabio Wanderley » Sex Nov 30, 2012 09:23
por Fabio Wanderley » Sex Nov 30, 2012 09:23
Bom dia, Sherminator,
Eu fiz uma resolução aqui. Você tem a resposta? Encontrei que
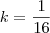
. É isso?
Se for, postarei a resolução para que os colegas a analisem.
Até mais!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por Sherminator » Sex Nov 30, 2012 12:35
por Sherminator » Sex Nov 30, 2012 12:35
Boa tarde, não tenho a resposta, este foi um exercício que saiu num exame que não consegui resolver.
Vou dar uma olhadela nesse livro que sugeriu, obrigado

Pode postar a sua resolução se faz favor?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estudo da [continuidade] de uma função
por Teh_eng » Qui Mai 03, 2012 13:43
- 1 Respostas
- 1373 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 14:52
Cálculo: Limites, Derivadas e Integrais
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:17
- 2 Respostas
- 2096 Exibições
- Última mensagem por adauto martins

Qui Dez 18, 2014 11:43
Geometria Analítica
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:21
- 0 Respostas
- 1358 Exibições
- Última mensagem por Livingstone

Sex Dez 12, 2014 15:21
Geometria Analítica
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:27
- 1 Respostas
- 1569 Exibições
- Última mensagem por adauto martins

Ter Dez 16, 2014 10:43
Geometria Analítica
-
- Estudo das funções
por Cleyson007 » Dom Out 26, 2008 21:58
- 5 Respostas
- 6494 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:44
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. na equação para
na equação para  e
e  na equação para
na equação para 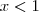 . Em seguida iguale as duas e isole o valor
. Em seguida iguale as duas e isole o valor  .
.
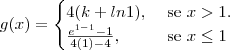

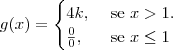
 , faz-me bastante confusão.
, faz-me bastante confusão.

 .
.
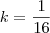 . É isso?
. É isso?


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
