 por Jhenrique » Sex Nov 16, 2012 02:49
por Jhenrique » Sex Nov 16, 2012 02:49
A interpretação para a razão entre duas grandezas é a de "
taxa de variação", que, para mim, é uma interpretação muito abrangente e excelente! Mas o que eu não entendo é o produto entre duas grandezas que geralmente é explicado como a área da
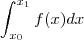
, tal explicação faz sentido para mim quando as grandezas

e

são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por LuizAquino » Sáb Nov 17, 2012 10:12
por LuizAquino » Sáb Nov 17, 2012 10:12
Jhenrique escreveu:A interpretação para a razão entre duas grandezas é a de "
taxa de variação", que, para mim, é uma interpretação muito abrangente e excelente! Mas o que eu não entendo é o produto entre duas grandezas que geralmente é explicado como a área da
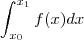
, tal explicação faz sentido para mim quando as grandezas

e

são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!
Considere os dois problemas abaixo.
Problema 1) Duas pessoas possuem cada uma 5 balas. Quantas balas elas possuem juntas?
Problema 2) Um retângulo possui lados medindo 2 cm e 5 cm. Qual é a área desse retângulo?
É fácil obter que a reposta desses problemas são, respectivamente, 10 balas e 10 cm².
Obviamente a grandeza "bala" é diferente da grandeza "cm²". Entretanto, em ambos os problemas a reposta é algo como: 10 unidades de "grandeza", onde a palavra "grandeza" pode ser substituída por "bala" ou por "cm²" conforme o caso. Nesse sentido, podemos afirmar que: encontrar a quantidade da grandeza no problema 1 é equivalente a encontrar a quantidade da grandeza no problema 2.
Podemos transpor essa ideia para o caso da integral que você citou. Suponha que a grandeza A é definida como o produto entre as grandezas B e C, isto é, por definição temos A = BC. Suponha ainda que certa função f contínua (e positiva) associa a grandeza B com a grandeza C. Desse modo, achar a quantidade da grandeza A quando a grandeza B varia no intervalo
![[b_0,\, b_1] [b_0,\, b_1]](/latexrender/pictures/1889e92cc0c025726fcda51918aae93a.png)
e a grandeza C varia conforme f no intervalo
![[f(b_0),\,f(b_1)] [f(b_0),\,f(b_1)]](/latexrender/pictures/5e0606543d5374f2647692cae88c76f5.png)
(ou
![[f(b_1),\,f(b_0)] [f(b_1),\,f(b_0)]](/latexrender/pictures/70a68dd7f9e97806ad5c0fc6ce79681d.png)
, caso

), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Jhenrique » Seg Nov 19, 2012 03:33
por Jhenrique » Seg Nov 19, 2012 03:33
O que mais me dá um nó na cabeça é que as vezes, no meu curso de técnico em mecânica, preciso calcular o momento estático e o momento de inércia de uma secção e estas grandezas são dimensionadas como

e

, respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz
sexta para determinar o diâmetro de um eixo...
Penso que deveria existir alguma teoria conceitual para explicar isso, algo como distinguir o coeficiente, junto com o seu próprio expoente, da parte literal, assim, a parte adjetiva não se misturaria com a parte substantiva. Sei lá... enfim... é devido a essa confusão que vim a procura de alguma luz.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por LuizAquino » Seg Nov 19, 2012 10:27
por LuizAquino » Seg Nov 19, 2012 10:27
Jhenrique escreveu:O que mais me dá um nó na cabeça é que as vezes, no meu curso de técnico em mecânica, preciso calcular o momento estático e o momento de inércia de uma secção e estas grandezas são dimensionadas como

e

, respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz sexta para determinar o diâmetro de um eixo...
Penso que deveria existir alguma teoria conceitual para explicar isso, algo como distinguir o coeficiente, junto com o seu próprio expoente, da parte literal, assim, a parte adjetiva não se misturaria com a parte substantiva. Sei lá... enfim... é devido a essa confusão que vim a procura de alguma luz.
O seu problema é comum para todos os seres humanos: não somos capazes de enxergar quatro dimensões. O nosso sistema ocular apenas consegue enxergar 3 dimensões. É devido a essa limitação biológica que isso lhe "dá um nó na cabeça". Entretanto, apesar dessa limitação visual, não há problema teórico algum em trabalhar com 4 (ou até n) dimensões.
Além disso, geralmente nos cursos técnicos apenas são fornecidas fórmulas prontas (ou tabelas). Mas essas fórmulas (ou tabelas) prontas não "caíram do céu". Tipicamente a obtenção delas é estudada nos cursos de Engenharia, nas disciplinas de Física ou de Cálculo. Procure por esses conteúdos nessas disciplinas. Ao estudar a maneira como os cálculos são obtidos você entenderá melhor a dimensão dessas grandezas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2057 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- relação entre x e y
por Apotema » Qua Nov 18, 2009 19:57
- 4 Respostas
- 5860 Exibições
- Última mensagem por Apotema

Seg Nov 23, 2009 08:12
Trigonometria
-
- relação entre a e b
por jose henrique » Seg Set 13, 2010 09:31
- 3 Respostas
- 4712 Exibições
- Última mensagem por Elcioschin

Ter Set 14, 2010 10:45
Álgebra Elementar
-
- [relação entre PA e PG]
por JKS » Qui Abr 11, 2013 01:11
- 2 Respostas
- 3480 Exibições
- Última mensagem por JKS

Dom Abr 21, 2013 18:07
Progressões
-
- relação entre conjuntos
por Julivanny » Sex Set 12, 2008 12:46
- 1 Respostas
- 3440 Exibições
- Última mensagem por admin

Ter Set 16, 2008 17:44
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
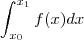 , tal explicação faz sentido para mim quando as grandezas
, tal explicação faz sentido para mim quando as grandezas  e
e  são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!
são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!

![[b_0,\, b_1] [b_0,\, b_1]](/latexrender/pictures/1889e92cc0c025726fcda51918aae93a.png) e a grandeza C varia conforme f no intervalo
e a grandeza C varia conforme f no intervalo ![[f(b_0),\,f(b_1)] [f(b_0),\,f(b_1)]](/latexrender/pictures/5e0606543d5374f2647692cae88c76f5.png) (ou
(ou ![[f(b_1),\,f(b_0)] [f(b_1),\,f(b_0)]](/latexrender/pictures/70a68dd7f9e97806ad5c0fc6ce79681d.png) , caso
, caso  ), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral
), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral  .
.
 e
e  , respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz
, respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz