[INTEGRAL DEFINIDA] Exercício do Enade 2011

por **fabriel** » Seg Nov 05, 2012 13:49

E ai galera blz. então é dado o exercício ai:

#Considere a função f:R-R definida por
$y=f(x)={x}^{4}-{5x}^{2}+4$
para cada xeR. A área da região limitada pelo gráfico
da função y=f(x), o eixo Ox e as retas x=0 e x=2
é igual a.

Resolvendo a integral:
$\int_{0}^{2}{x}^{4}-{5x}^{2}+4dx$

Vamos obter:
$\left[\frac{{x}^{5}}{5}-\frac{{5x}^{3}}{3}+4x \right]$ Avaliado nos pontos 0 e 2. obtemos então: $\frac{16}{15}$

Mas pelo que vi no gabarito a resposta certa é: $\frac{60}{15}$

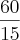
E não entendi o que eu errei..Poderiam me ajudar nessa questão.

por **MarceloFantini** » Seg Nov 05, 2012 15:22

A curva tem uma raíz em x=1

e passa a ser negativa. Normalmente quando integramos esta área é considerada "negativa" pelo fato de estar orientada "negativamente". Para obter o valor absoluto da área sob a curva, integre de 0 a 1 normalmente e depois tome o módulo da integral de 1 a 2. O resultado será como está no gabarito.

Veja aqui o que eu quero dizer.