 por mayconf » Sex Out 26, 2012 16:06
por mayconf » Sex Out 26, 2012 16:06
![y=tg\sqrt[3]{5-6x} y=tg\sqrt[3]{5-6x}](/latexrender/pictures/7e720dabf50ad4227b9a9e1e8e39e085.png)
Sendo:
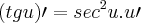
minha professora resolveu assim:
![y= tg\sqrt[3]{5-6x}=\left(tg\left(5-6x \right){}^{\frac{1}{2}} \right){}^{3} y= tg\sqrt[3]{5-6x}=\left(tg\left(5-6x \right){}^{\frac{1}{2}} \right){}^{3}](/latexrender/pictures/ee2f23e99ac0c80c02754af61490d910.png)
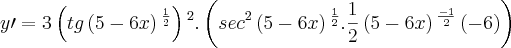
eu num intendi quele menus 6 no fim ali
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Out 27, 2012 08:24
por MarceloFantini » Sáb Out 27, 2012 08:24
Está errado. Note que
![\sqrt[3]{5-6x} = (5-6x)^{\frac{1}{3}} \sqrt[3]{5-6x} = (5-6x)^{\frac{1}{3}}](/latexrender/pictures/84bee94d0776fff074a63c7cf69b9009.png)
, que é diferente de
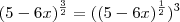
.
Note que você tem a composição de três funções:
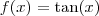
,
![h(x) = \sqrt[3]{x} h(x) = \sqrt[3]{x}](/latexrender/pictures/d6b13534bd22fae9d60908d58e9c5a5a.png)
e
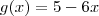
. A composição é

, e derivando teremos
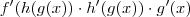
pela regra da cadeia. Portanto,
![(\tan (\sqrt[3]{5-6x}))' = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (5-6x)' (\tan (\sqrt[3]{5-6x}))' = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (5-6x)'](/latexrender/pictures/887521cf100f940931e2c6ef1e300af4.png)
![= \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (-6) = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (-6)](/latexrender/pictures/e1fc3a3d8911e785dedb9d47d8c5f32b.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10886 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13191 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14795 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5113 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y=tg\sqrt[3]{5-6x} y=tg\sqrt[3]{5-6x}](/latexrender/pictures/7e720dabf50ad4227b9a9e1e8e39e085.png)
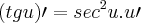
![y= tg\sqrt[3]{5-6x}=\left(tg\left(5-6x \right){}^{\frac{1}{2}} \right){}^{3} y= tg\sqrt[3]{5-6x}=\left(tg\left(5-6x \right){}^{\frac{1}{2}} \right){}^{3}](/latexrender/pictures/ee2f23e99ac0c80c02754af61490d910.png)
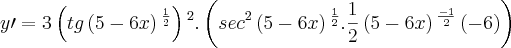

![\sqrt[3]{5-6x} = (5-6x)^{\frac{1}{3}} \sqrt[3]{5-6x} = (5-6x)^{\frac{1}{3}}](/latexrender/pictures/84bee94d0776fff074a63c7cf69b9009.png) , que é diferente de
, que é diferente de 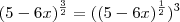 .
.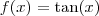 ,
, ![h(x) = \sqrt[3]{x} h(x) = \sqrt[3]{x}](/latexrender/pictures/d6b13534bd22fae9d60908d58e9c5a5a.png) e
e 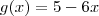 . A composição é
. A composição é  , e derivando teremos
, e derivando teremos 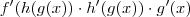 pela regra da cadeia. Portanto,
pela regra da cadeia. Portanto,![(\tan (\sqrt[3]{5-6x}))' = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (5-6x)' (\tan (\sqrt[3]{5-6x}))' = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (5-6x)'](/latexrender/pictures/887521cf100f940931e2c6ef1e300af4.png)
![= \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (-6) = \sec^2 (\sqrt[3]{5-6x}) \cdot \frac{1}{3} \frac{1}{\sqrt[3]{(5-6x)^2}} \cdot (-6)](/latexrender/pictures/e1fc3a3d8911e785dedb9d47d8c5f32b.png) .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
