por Arlan » Sex Set 10, 2010 14:42
Estou cursando o segundo período de Engenharia Civil e pagando a disciplina Cálculo I. Estou resolvendo as questões do Livro "O Cálculo com Geometria Analítica" de Louis Leithold.
Estou encontrando dificuldades na solução desta questão...
![\lim_{h\rightarrow 0} \frac{\sqrt[3]{h+1}-1}{h}](/latexrender/pictures/05d370c790a33a278a0fca6949754f39.png "\lim_{h\rightarrow 0} \frac{\sqrt[3]{h+1}-1}{h}")
Adotei as seguintes estratégias de resolução:
( i ) coloquei o -1 do numerador dentro da raíz cúbica
(ii) somei 1 e subtrai -1 ao denominador (h+1)-1
![\lim_{h\rightarrow0}\frac{\sqrt[3]{h + 1} - \sqrt[3]{1}}\left(\sqrt[3]{h + 1}\right){}^{3} - \left(\sqrt[3]{1} \right){}^{3}](/latexrender/pictures/239b2e05f131af20070453c87068953d.png "\lim_{h\rightarrow0}\frac{\sqrt[3]{h + 1} - \sqrt[3]{1}}\left(\sqrt[3]{h + 1}\right){}^{3} - \left(\sqrt[3]{1} \right){}^{3}")
-
Arlan
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Qui Set 09, 2010 21:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelando em Engenharia
- Andamento: cursando
por Marcampucio » Sex Set 10, 2010 16:12
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário
-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 4995 Exibições
- Última mensagem por LuizAquino
Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4317 Exibições
- Última mensagem por LuizAquino
Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4557 Exibições
- Última mensagem por umbrorz
Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4075 Exibições
- Última mensagem por e8group
Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2648 Exibições
- Última mensagem por DanielFerreira
Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
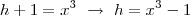
![\\\lim_{h\to0}\frac{\sqrt[3]{h+1}-1}{h}=\lim_{x\to1}\frac{x-1}{x^3-1} =\lim_{x\to1}\frac{x-1}{(x-1)(x^2+1+x)}\\\\\\\lim_{x\to1}\frac{1}{x^2+1+x} =\frac{1}{3}](/latexrender/pictures/8999fd5b48411f24568e829431676eb5.png "\\\lim_{h\to0}\frac{\sqrt[3]{h+1}-1}{h}=\lim_{x\to1}\frac{x-1}{x^3-1} =\lim_{x\to1}\frac{x-1}{(x-1)(x^2+1+x)}\\\\\\\lim_{x\to1}\frac{1}{x^2+1+x} =\frac{1}{3}")