Sobre as 3 questões (ultima postagem):
1)
Se formos determinar as superfícies de nível neste caso teremos planos no R³.
Lembrando a equação geral do plano:
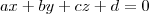
Podemos ver isso achando algumas destas superfícies, veja:

Como podemos ver estas superfícies tem formulação semelhante a eq. geral do plano.
2)
A equação geral de elipses é:
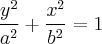
, sendo "a" a ordenada e "b" a abscissa.
O enunciado pede a curva de nivel 4, portanto teremos:

Logo elipse com ordenada 4 e abscissa 3 (Letra E).
3) Nessa não entendi o que está escrito no enunciado "...conjunto dos pontos em que ? ...".
Mas o grafico desta função lembra uma cela de cavalo, pode ver no link abaixo.
https://www.google.com/search?q=x%5E2-y%5E2&client=firefox-b&source=lnms&sa=X&ved=0ahUKEwiMw-W38JPeAhUBgpAKHWqEAxAQ_AUICSgA&biw=1366&bih=650&dpr=1Sobre a outra postagem:
4)
Pela equação é possível identifica-la como uma elipse.
Podemos "arrumar" a equação da seguinte forma:
![\\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\ \\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\](/latexrender/pictures/20ed23358145249fc83094d2baaa0475.png)
Se fizermos a troca:
![\\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\ \\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\](/latexrender/pictures/3caf55b1054e4777fd6e8a1bb38c661f.png)
Ficamos com A² + B² = 1
Podemos ver a semelhança entre essa formulação e a identidade trigonométrica cos²t + sen²t = 1.
Vamos então "forçar" esta semelhança:
![\\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\ \\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\](/latexrender/pictures/655f18a5d5496770aca2866512d6ff38.png)
Resp:
![\gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right) \gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right)](/latexrender/pictures/33fdf4861c71943c19d768a4e85c89ad.png)
3)
Precisamos lembrar que nas funções reais só podemos ter valores maiores ou iguais a zero, logo:
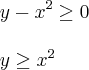
Como podemos ver o domínio da função f(x,y) está acima da parábola y=x².
Como a imagem da função está no R³ e não temos restrições para z, o domínio será então uma "calha" formada por parábolas y=x² ao longo do eixo z.









![f(x,y)=\sqrt[2]{y-{x}^{2}} f(x,y)=\sqrt[2]{y-{x}^{2}}](/latexrender/pictures/8af62dc12323ad7dbd37b8bdcad34037.png)


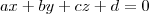

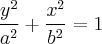 , sendo "a" a ordenada e "b" a abscissa.
, sendo "a" a ordenada e "b" a abscissa.
![\\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\ \\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\](/latexrender/pictures/20ed23358145249fc83094d2baaa0475.png)
![\\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\ \\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\](/latexrender/pictures/3caf55b1054e4777fd6e8a1bb38c661f.png)
![\\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\ \\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\](/latexrender/pictures/655f18a5d5496770aca2866512d6ff38.png)
![\gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right) \gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right)](/latexrender/pictures/33fdf4861c71943c19d768a4e85c89ad.png)
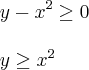

 . Sobre o conjunto dos pontos em que vale , é correto afirmar:
. Sobre o conjunto dos pontos em que vale , é correto afirmar:





 Muito muito obrigado !!!
Muito muito obrigado !!!
![\frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}} \frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}}](/latexrender/pictures/75bc11fbba7efd7b60797a155deecf34.png) ? (segue anexo o exercício)
? (segue anexo o exercício)
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) chega-se no formato da alternativa.
chega-se no formato da alternativa.![\\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent \\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent](/latexrender/pictures/bcc68a0619e8c851374465ab64d2bec3.png)









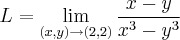
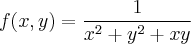
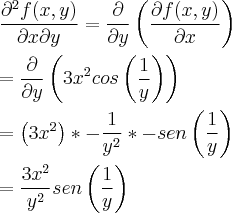





 Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!
Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!





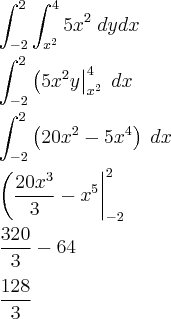








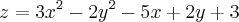 , descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).
, descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).







