Determine os pontos de máximo e mínimo locais da função
 , dizendo quais destes pontos são máximos ou mínimos globais.
, dizendo quais destes pontos são máximos ou mínimos globais.O que eu fiz para encontrar os pontos de mínimo locais:
1º - Derivei a função:

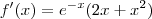
2º - Igualei a função a zero para encontrar os pontos críticos:
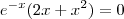
Como
 é sempre positivo, a função só poderá ser zero quando
é sempre positivo, a função só poderá ser zero quando 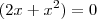 . Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.
. Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.3º - Calculei a f'(x) para -3 , -1 e 1 para saber se a função é crescente ou decrescente antes e depois dos pontos críticos.
 (positivo)
(positivo)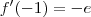 (negativo)
(negativo)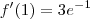 (positivo)
(positivo)4º - Determinei os pontos de mínimo e máximo locais:
Como a função é crescente antes de -2 e decrescente após o -2, logo ele é um ponto de máximo local.
E como a função é decrescente antes do 0 e crescente após 0 , ele é um ponto de mínimo local.
A partir de agora eu não sei o que devo fazer para encontrar os pontos de máximo e mínimo globais, caso existam.
Obs: O gabarito da questão informa que a função não possui máximo global e que o ponto 0 é mínimo global.



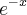 pela regra
pela regra 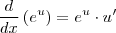 obtemos
obtemos  .
.
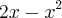 são 0 e 2.
são 0 e 2.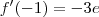 (negativo, portanto decrescente)
(negativo, portanto decrescente) (positivo, portanto crescente)
(positivo, portanto crescente) (negativo, portanto decrescente)
(negativo, portanto decrescente) da derivada da função original que usamos para encontrar os pontos críticos é uma parábola. Nos intervalos onde esta parábola tem imagem negativa, a função original é decrescente. No intervalo onde esta parábola tem imagem positiva, a função original é crescente. O
da derivada da função original que usamos para encontrar os pontos críticos é uma parábola. Nos intervalos onde esta parábola tem imagem negativa, a função original é decrescente. No intervalo onde esta parábola tem imagem positiva, a função original é crescente. O  nem
nem  , que é maior que 2. Portanto, 2 é máximo local.
, que é maior que 2. Portanto, 2 é máximo local.

 .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.