

![\lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} \lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}}](/latexrender/pictures/95767d850ccd39bf08d6540052a72c3f.png)
Conto com a ajuda de vocÊs. Obrigada.




![\lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} \lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}}](/latexrender/pictures/95767d850ccd39bf08d6540052a72c3f.png)




lunayanne escreveu:Olá! Eu tenho um pouco de dificuldade com limites e gostaria de ajuda para resolver alguns:
Conto com a ajuda de vocÊs. Obrigada.
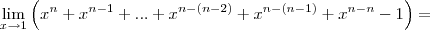
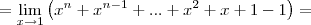
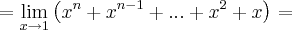


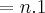
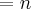 .
.![\lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} \lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}}](/latexrender/pictures/6d8b8b57d56a1bb727d2abbfc895c754.png)
![\sqrt[6]{x} = k \sqrt[6]{x} = k](/latexrender/pictures/ed9facde3b125cd8c99991c049f529b6.png) , temos que
, temos que ![\sqrt[6]{x^2} = k^2 \sqrt[6]{x^2} = k^2](/latexrender/pictures/18f69ff7d550e3a6e09e7ed55e3da404.png) e
e ![\sqrt[6]{x^3} = k^3 \sqrt[6]{x^3} = k^3](/latexrender/pictures/1904f6b30e514f0d8fa5e66eb299183d.png) . E se
. E se 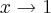 , então
, então ![k\rightarrow\sqrt[3]{1} = 1 k\rightarrow\sqrt[3]{1} = 1](/latexrender/pictures/145c29c1ac9a425e368d56dfa476eece.png) . Aí ficamos com:
. Aí ficamos com:![\lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3} \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3}](/latexrender/pictures/41cbbf22a00ced820b847d82a78bb40f.png)
 . Logo, temos:
. Logo, temos: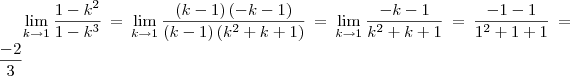 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.



