Luciano Dias escreveu:Tenho pesquisado sobre o tema, que na teoria parece fácil, mas que os livros e páginas da internet não vão direto ao assunto.
Não quero abusar aqui deixando várias perguntas em um mesmo tópico, mas é inevitável se tratando do mesmo assunto, pois realmente existem dúvidas sobre o assunto. Estudar sozinho é desse jeito.
- Como saber se uma função possui assíntotas verticais e/ou horizontais e determinar as suas equações.
Por exemplo, na função f(x) =2x^2 + 1/2x^2 -3x
Boa tarde.
Você falou que está estudando sozinho. Está seguindo algum livro?
Pois bem, para saber se uma função

possui
assíntotas verticais em alguma reta

, basta calcular o limite de

, com x tendendo a

. Matemáticamente, você fará

.

será uma assíntota vertical se esse limite der

Exemplo: A reta

é uma assíntota vertical da curva

, pois

Agora para saber se a função

possui
assíntotas horizontais em alguma reta

, calcularemos o limite de

com x tendendo ao mais e menos infinito. Matemáticamente, você fará

. O resultado

e

deste limite será assíntota horizontal.
Exemplo: A reta

é uma assíntota horizontal da curva
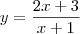
, pois
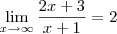
e
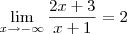
Lembrando que estas assíntotas horizontais que encontramos (2) nao precisa ser iguais. Neste caso esta curva possui apenas uma assíntota horizontal.



 possui
possui  , basta calcular o limite de
, basta calcular o limite de  . Matemáticamente, você fará
. Matemáticamente, você fará  .
. 
 é uma assíntota vertical da curva
é uma assíntota vertical da curva  , pois
, pois 
 possui
possui  , calcularemos o limite de
, calcularemos o limite de  . O resultado
. O resultado  e
e  deste limite será assíntota horizontal.
deste limite será assíntota horizontal. é uma assíntota horizontal da curva
é uma assíntota horizontal da curva 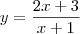 , pois
, pois 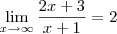 e
e 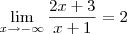


 .
. ,
,  e para
e para  ,
,  .
.
 por
por  .
.
