 por fisicanaveia » Sáb Ago 16, 2014 00:21
por fisicanaveia » Sáb Ago 16, 2014 00:21
Quais são todas as possibilidades da inexistência de um limite ? Eu sei que o limite não existe quando os limites laterais são diferentes, mas existem outros motivos ?
-
fisicanaveia
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Ago 16, 2014 00:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Man Utd » Sáb Ago 16, 2014 18:42
por Man Utd » Sáb Ago 16, 2014 18:42
fisicanaveia escreveu:Quais são todas as possibilidades da inexistência de um limite ? Eu sei que o limite não existe quando os limites laterais são diferentes, mas existem outros motivos ?
Sim existe outros como por exemplo :
lim x->infinito senx=valor indefinido entre -1 e 1
pois quando "x" tende a mais infinito a função seno ficará oscilando em -1 e 1.Logo não existe limite, pois se existisse o limite seria um valor real único.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por fisicanaveia » Sáb Ago 16, 2014 22:57
por fisicanaveia » Sáb Ago 16, 2014 22:57
Ok. Então, considerando :
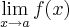
, podemos dizer, generalizando, que quando os valores de f(x) não tendem a um n° fixo quando x tende a 'a' , aí o Limite não existe ?! Mas tirando isso, não existe nenhum outro caso ?
-
fisicanaveia
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Ago 16, 2014 00:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Man Utd » Dom Ago 17, 2014 12:37
por Man Utd » Dom Ago 17, 2014 12:37
fisicanaveia escreveu:Ok. Então, considerando :
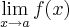
, podemos dizer, generalizando, que quando os valores de f(x) não tendem a um n° fixo quando x tende a 'a' , aí o Limite não existe ?!
Sim.Se existir o limite, o limite tem que ser único.
fisicanaveia escreveu:Mas tirando isso, não existe nenhum outro caso ?
Existe os casos de quando "x" tende a valores que não estão no domínio, mas esse caso recai em limites laterais diferentes :
lim x->0

observe que quando "x" tende a valores maiores que 0 , o limite é zero, mas quando "x" tende a valores menores que 0 (isto é valores negativos), o limite não existe pois a função raiz quadrada de x só está definida para [0,+infinito) .
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por fisicanaveia » Seg Ago 25, 2014 20:11
por fisicanaveia » Seg Ago 25, 2014 20:11
Então, voltaria a questão de limites diferentes ?
-
fisicanaveia
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Ago 16, 2014 00:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Man Utd » Qua Ago 27, 2014 19:15
por Man Utd » Qua Ago 27, 2014 19:15
fisicanaveia escreveu:Então, voltaria a questão de limites diferentes ?
De certa maneira sim.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- A expressão abaixo expressa a inexistência de um limite?
 por Douglas16 » Sáb Mar 02, 2013 13:23
por Douglas16 » Sáb Mar 02, 2013 13:23
- 2 Respostas
- 1486 Exibições
- Última mensagem por Douglas16

Sáb Mar 02, 2013 19:38
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5114 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7249 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




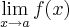 , podemos dizer, generalizando, que quando os valores de f(x) não tendem a um n° fixo quando x tende a 'a' , aí o Limite não existe ?! Mas tirando isso, não existe nenhum outro caso ?
, podemos dizer, generalizando, que quando os valores de f(x) não tendem a um n° fixo quando x tende a 'a' , aí o Limite não existe ?! Mas tirando isso, não existe nenhum outro caso ?
, podemos dizer, generalizando, que quando os valores de f(x) não tendem a um n° fixo quando x tende a 'a' , aí o Limite não existe ?!






 , avisa que eu resolvo.
, avisa que eu resolvo.

