bom,vamos a soluçao correta desse exercicio;colocarei aqui de forma sucinta,considerando os pontos mais importantes,e deixo a cargo dos colegas os algebrismo q. conduzem a resposta...
considerando,como antes descrito,a barra tem o ponto de partida do corredor "a",passa pelo ponto interno da quina e vai ate o corredor"b"...podemos tomar ai 2 triang.retangulos,cujas hipotenusas dao o comprimento da barra;vamos tomar a barra em funçao do angulo q. os triangulos fazem com a horizontal,no caso do corredor "a",sera a parede interna,no caso do corredor "b"sera o comprim. do corredor...entao:

...tomamos a dL/d

=asec

tg

-bcossec

cotg

=0

a
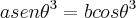
...tomando, cos

=
![\sqrt[]{1-({sen\theta}^{2})} \sqrt[]{1-({sen\theta}^{2})}](/latexrender/pictures/5a98ee06bbb9ce733174e73d477203e0.png)

,entao
![\Rightarrow a{sen\theta}^{3}=b({\sqrt[]{1-({sen\theta})^{2}}})^{3}\Rightarrow {sen\theta}^{2}(\sqrt[3]{({a/b})^{2}})+1)=1\Rightarrow {sen\theta}^{2}=1/((\sqrt[3]{({a/b})^{2}})+1) \Rightarrow a{sen\theta}^{3}=b({\sqrt[]{1-({sen\theta})^{2}}})^{3}\Rightarrow {sen\theta}^{2}(\sqrt[3]{({a/b})^{2}})+1)=1\Rightarrow {sen\theta}^{2}=1/((\sqrt[3]{({a/b})^{2}})+1)](/latexrender/pictures/af5e7674ec602b1ac522eed64322f314.png)
,voltando em

=(a/cos

)+(b/sen

)=(
![(a/\sqrt[]{1-{sen\theta}^{2}})+(b/(sen\theta})) (a/\sqrt[]{1-{sen\theta}^{2}})+(b/(sen\theta}))](/latexrender/pictures/c0e2868088ed28ed029e019fed7f8755.png)
=(
![a/\sqrt[3]{{a/b}})+(b/(\sqrt[2]{1+{\sqrt[3]({a/b}})^{2}})) a/\sqrt[3]{{a/b}})+(b/(\sqrt[2]{1+{\sqrt[3]({a/b}})^{2}}))](/latexrender/pictures/d2c1994c8e164a7c3674597ed728158e.png)
,faz.k=
![\sqrt[3]{a/b} \sqrt[3]{a/b}](/latexrender/pictures/12e844cc1b6555d6a93c6ed081e7d09a.png)
,teremos...L=(a/k)+b(1/((1+

),resolvendo os algebrismos e etc...,chegamos em L=
![\sqrt[3]{({a}^{2/3}+{b}^{2/3})^2} \sqrt[3]{({a}^{2/3}+{b}^{2/3})^2}](/latexrender/pictures/a72712791ab69c98dc2d8a889596cebe.png)
,q. e a resposta certa,a qual conferi no livro de calculo(um curso universitario),edwie moise,o q. realmente me animou a resolver esse exercicio...voltando em

,tomando

,caso do nosso triang.retangulo isosceles de hipotenusa minima L=
![\sqrt[]{2}(a+b) \sqrt[]{2}(a+b)](/latexrender/pictures/4050a8a54c3c725d1d9de8efedc79bd9.png)
,q. seria o comprim. minimo p/ L...minha resposta anterior...ujaaaaaa....



 ...como
...como =
=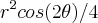 =0
=0 ...logo o triangulo retangulo e isosceles...CQP...
...logo o triangulo retangulo e isosceles...CQP...![sen(\pi/4)=a/x,a e o comprim. do cateo do triangulo do corredor "a"...logo x=\sqrt[2]{2}.a sen(\pi/4)=a/x,a e o comprim. do cateo do triangulo do corredor "a"...logo x=\sqrt[2]{2}.a](/latexrender/pictures/2255dd286c25ea93a3d99339b468b922.png) ...o mesmo raciocinio se faz com o outro tringulo...o compr.total da barra sera
...o mesmo raciocinio se faz com o outro tringulo...o compr.total da barra sera ![L=\sqrt[2]{2}(a+b) L=\sqrt[2]{2}(a+b)](/latexrender/pictures/de52592998966711a44e90f22d66ec05.png)

 ...tomamos a dL/d
...tomamos a dL/d a
a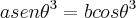 ...tomando, cos
...tomando, cos![\sqrt[]{1-({sen\theta}^{2})} \sqrt[]{1-({sen\theta}^{2})}](/latexrender/pictures/5a98ee06bbb9ce733174e73d477203e0.png)
 ,entao
,entao ![\Rightarrow a{sen\theta}^{3}=b({\sqrt[]{1-({sen\theta})^{2}}})^{3}\Rightarrow {sen\theta}^{2}(\sqrt[3]{({a/b})^{2}})+1)=1\Rightarrow {sen\theta}^{2}=1/((\sqrt[3]{({a/b})^{2}})+1) \Rightarrow a{sen\theta}^{3}=b({\sqrt[]{1-({sen\theta})^{2}}})^{3}\Rightarrow {sen\theta}^{2}(\sqrt[3]{({a/b})^{2}})+1)=1\Rightarrow {sen\theta}^{2}=1/((\sqrt[3]{({a/b})^{2}})+1)](/latexrender/pictures/af5e7674ec602b1ac522eed64322f314.png) ,voltando em
,voltando em ![(a/\sqrt[]{1-{sen\theta}^{2}})+(b/(sen\theta})) (a/\sqrt[]{1-{sen\theta}^{2}})+(b/(sen\theta}))](/latexrender/pictures/c0e2868088ed28ed029e019fed7f8755.png) =(
=(![a/\sqrt[3]{{a/b}})+(b/(\sqrt[2]{1+{\sqrt[3]({a/b}})^{2}})) a/\sqrt[3]{{a/b}})+(b/(\sqrt[2]{1+{\sqrt[3]({a/b}})^{2}}))](/latexrender/pictures/d2c1994c8e164a7c3674597ed728158e.png) ,faz.k=
,faz.k=![\sqrt[3]{a/b} \sqrt[3]{a/b}](/latexrender/pictures/12e844cc1b6555d6a93c6ed081e7d09a.png) ,teremos...L=(a/k)+b(1/((1+
,teremos...L=(a/k)+b(1/((1+ ),resolvendo os algebrismos e etc...,chegamos em L=
),resolvendo os algebrismos e etc...,chegamos em L=![\sqrt[3]{({a}^{2/3}+{b}^{2/3})^2} \sqrt[3]{({a}^{2/3}+{b}^{2/3})^2}](/latexrender/pictures/a72712791ab69c98dc2d8a889596cebe.png) ,q. e a resposta certa,a qual conferi no livro de calculo(um curso universitario),edwie moise,o q. realmente me animou a resolver esse exercicio...voltando em
,q. e a resposta certa,a qual conferi no livro de calculo(um curso universitario),edwie moise,o q. realmente me animou a resolver esse exercicio...voltando em  ,caso do nosso triang.retangulo isosceles de hipotenusa minima L=
,caso do nosso triang.retangulo isosceles de hipotenusa minima L=![\sqrt[]{2}(a+b) \sqrt[]{2}(a+b)](/latexrender/pictures/4050a8a54c3c725d1d9de8efedc79bd9.png) ,q. seria o comprim. minimo p/ L...minha resposta anterior...ujaaaaaa....
,q. seria o comprim. minimo p/ L...minha resposta anterior...ujaaaaaa....![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.