[INTEGRAL DUPLA] Área do conjunto de integração

por **Matemagica** » Sáb Dez 14, 2013 05:31

É possível calcular a área da região B delimitada pelas curvas x = y² + 1 e x + y = 3? Se sim, calcule.

Sei que posso encontrar a área do conjunto de integração B através da integral dupla da função constante f(x,y) = 1, assim:
${A}_{B}=\int_{} \int_{B} 1 dx dy$

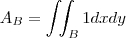
mas como calcular a área compreendida entre essas curvas?
Quer dizer, como transformo a área entre elas no meu conjunto B?

Pensei em fazer a interseção delas, para ver onde se encontram.. fiz isso:

$y = {x}^{2} + 1 x + y = 3 \Rightarrow x + ({x}^{2} + 1) = 3 \Rightarrow {x}^{2} + x - 2 = 0$

$\Rightarrow x = 1$ ou x = -2

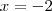
assim, vai estar variando em [-2,1] em x.

e y variando entre as funções,
$y = {x}^{2} + 1$
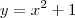
e
$x + y = 3 \Rightarrow y = 3 - x$

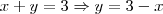
só que então, preciso descobrir qual curva está 'abaixo' e qual está 'em cima'.
para isso, peguei um valor entre x pertencente a ]-2,1[. por exemplo, x = 0

assim,
$y = {0}^{2} + 1 \Rightarrow y = 1$
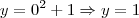
e
$y = 3 - 0 \Rightarrow y = 3$

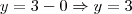
logo, varia em y, entre (nessa ordem)
$y = {x}^{2} + 1$
e
y = 3 - x

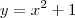
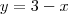
e aí, ficaria mais ou menos assim o cálculo dessa área:

$\int_{-2}^{1} \int_{{x}^{2} + 1}^{3 - x} dy dx$

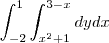
é isso mesmo, galera?
e se estiver correto, o que acharam da minha 'metodologia'? há um modo mais direto? o que vocês mudariam?

obrigado pela ajuda e aguardo sua resposta!!