Sei que posso encontrar a área do conjunto de integração B através da integral dupla da função constante f(x,y) = 1, assim:
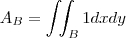
mas como calcular a área compreendida entre essas curvas?
Quer dizer, como transformo a área entre elas no meu conjunto B?
Pensei em fazer a interseção delas, para ver onde se encontram.. fiz isso:

 ou
ou 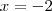
assim, vai estar variando em [-2,1] em x.
e y variando entre as funções,
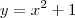
e
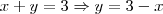
só que então, preciso descobrir qual curva está 'abaixo' e qual está 'em cima'.
para isso, peguei um valor entre x pertencente a ]-2,1[. por exemplo, x = 0
assim,
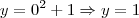
e
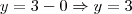
logo, varia em y, entre (nessa ordem)
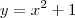
e
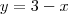
e aí, ficaria mais ou menos assim o cálculo dessa área:
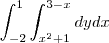
é isso mesmo, galera?
e se estiver correto, o que acharam da minha 'metodologia'? há um modo mais direto? o que vocês mudariam?
obrigado pela ajuda e aguardo sua resposta!!


 pela de
pela de  . Mas, já que vem a integral no exercício, você pode aplicá-la( como você fez) e perceber que os cálculos são s mesmo.
. Mas, já que vem a integral no exercício, você pode aplicá-la( como você fez) e perceber que os cálculos são s mesmo.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.