 por mthc10 » Qua Jul 24, 2013 01:08
por mthc10 » Qua Jul 24, 2013 01:08
Olá amigos, Boas,
Bom estou com um problema... Estou estudando pelo livro Leithold e fazendo seus respectivos exercícios, porém há algumas questão que eu não consigo resolver, e nem o livro soluciona questões semelhantes para eu ter noção de como resolver, e por isso peço a ajuda de vocês!

A questão é a seguinte:
"Ache a área da região limitada pela reta

e pela curva
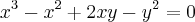
."
O livro apresenta uma sugestão para resolver tal problema, que seria o seguinte: "resolva a equação cúbica em y em termos de x e expresse y como duas funções de x.".
Bom, não consigo isolar X e Y dessa "função". Então não me ajudou muito tal sugestão.
O que eu (acho que)entendi é que para resolver esse problema, terei de achar os pontos onde essa curva intercepta a reta x = 4 e integrar essa curva sendo os limites de integração 0 e 4, visto que se x=0, y=0.
Alguém pode ajudar ? Obrigado desde já!
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 01:36
por Russman » Qua Jul 24, 2013 01:36
A curva mencionada não esta na forma

. Portanto, você deve tentar colocá-la assim. Para isto, visto que a forma implícita é uma forma cúbica em

você deve tentar resolvê-la para

ou resolvê-la para

percebendo que ela é uma forma quadática para

. Na primeira, você obterá
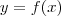
e na segunda

.
Repare que

de modo que

e temos duas soluções possíveis para

.
O gráfico dessas funções é

- graph
- graph (3).gif (5.66 KiB) Exibido 2680 vezes
de modo que a área delimitada por elas é bem visível. Eu acho que você terá de calcular a área da curva de cima de

até

e descontar da área da curva de baixo no mesmo intervalo. Descontar sim, pq de

até

a curva de baixo tem área positiva e em diante tem area negativa via integral. Daí, como no primeiro intervalo voce deve subtrair da área total e no segundo somar, os sinais se equilibram e voce tem o resultado de imediato.
Editado pela última vez por
Russman em Qua Jul 24, 2013 02:33, em um total de 2 vezes.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por mthc10 » Qua Jul 24, 2013 01:55
por mthc10 » Qua Jul 24, 2013 01:55
Desculpe a ignorância, mas como eu faço isso ?
Essa é a minha dificuldade, já que não consigo isolar as incógnitas... Se não consigo isolar as incógnitas, como vou resolver a equação em y ou em x ?
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
 por mthc10 » Qua Jul 24, 2013 13:02
por mthc10 » Qua Jul 24, 2013 13:02
Amigo, obrigado, consegui resolver graças a você!
É sim como você disse, Integral da função de cima
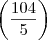
- integral da função de baixo

.
Como resultado:

Obrigado pela ajuda!
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Definida] Ex. do tipo "onde está o erro?"
por Fabio Wanderley » Seg Out 22, 2012 23:15
- 2 Respostas
- 2836 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:24
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para encontrar o "u" na integral
por vmouc » Sex Jun 10, 2011 15:25
- 3 Respostas
- 2418 Exibições
- Última mensagem por vmouc

Sáb Jun 11, 2011 21:05
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2865 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Seg Ago 22, 2011 00:44
- 1 Respostas
- 1428 Exibições
- Última mensagem por LuizAquino

Seg Ago 22, 2011 08:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 e pela curva
e pela curva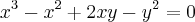 ."
."

 . Portanto, você deve tentar colocá-la assim. Para isto, visto que a forma implícita é uma forma cúbica em
. Portanto, você deve tentar colocá-la assim. Para isto, visto que a forma implícita é uma forma cúbica em  você deve tentar resolvê-la para
você deve tentar resolvê-la para  percebendo que ela é uma forma quadática para
percebendo que ela é uma forma quadática para 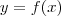 e na segunda
e na segunda  .
.

 até
até  a curva de baixo tem área positiva e em diante tem area negativa via integral. Daí, como no primeiro intervalo voce deve subtrair da área total e no segundo somar, os sinais se equilibram e voce tem o resultado de imediato.
a curva de baixo tem área positiva e em diante tem area negativa via integral. Daí, como no primeiro intervalo voce deve subtrair da área total e no segundo somar, os sinais se equilibram e voce tem o resultado de imediato.
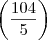 - integral da função de baixo
- integral da função de baixo  .
.