por Victor Gabriel » Sex Abr 26, 2013 20:51
por Victor Gabriel » Sex Abr 26, 2013 20:51
Olá pessoal boa noite, tem algum que pode mim ajuda nesta questão, olha com eu a fiz.
1º Calcule
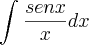
.
utilizei a tecnica da integração por parte:
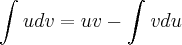
fazendo:

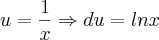
e

logo faço:
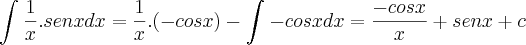
estou certo ou não?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Sex Abr 26, 2013 21:41
por e8group » Sex Abr 26, 2013 21:41
Acredito que não há funções elementares que derivando-se chega no integrando .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Gabriel » Sex Abr 26, 2013 22:22
por Victor Gabriel » Sex Abr 26, 2013 22:22
Santiago então como faço?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
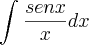 .
.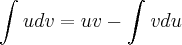

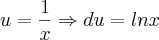 e
e  logo faço:
logo faço: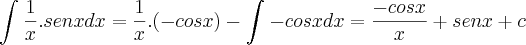

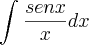 .
.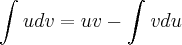

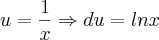 e
e  logo faço:
logo faço: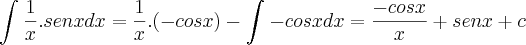



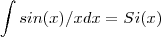 . Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .
. Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .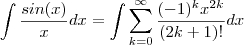 .Pela linearidade da integral ,
.Pela linearidade da integral ,