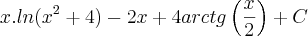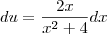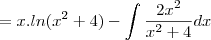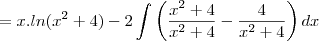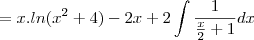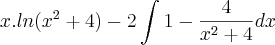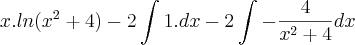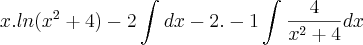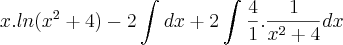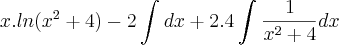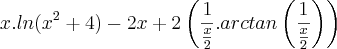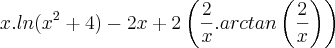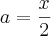por Matheus Lacombe O » Sex Mar 29, 2013 18:12
por Matheus Lacombe O » Sex Mar 29, 2013 18:12
Olá pessoal. Vou tentar ser o mais breve possível, dessa vez. O negócio é o seguinte:
-tentei resolver a questão:
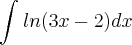
-Consegui, usando substituição para chamar "3x-2" de W. E somente depois aplicar a fórmula da integral por partes. Porque para mim assim fica mais fácil de entender.
- Até aí, tudo bem. O problema foi quando eu tentei resolver o exercício semelhante:
Dúvida: 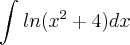
- Aqui, se eu chamo

de K, por exemplo, para poder usar a substituição. Desse jeito eu chamo "u" de "

" e "dv" de "
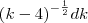
" Mas não dá certo!

- Eu sempre chego em algo parecido com:
![\frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right) \frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right)](/latexrender/pictures/cf4d5c1f673aac5a6b192656d1743349.png)
E, se é equivalente, eu não faço a menor idéia de como chegar na resposta do gabarito:
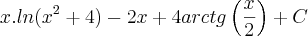 POR FAVOR GALERA. TEM COMO RESOLVE-LO USANDO SUBSTITUIÇÃO?
POR FAVOR GALERA. TEM COMO RESOLVE-LO USANDO SUBSTITUIÇÃO?Att. Matheus L. Oliveira
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por young_jedi » Sex Mar 29, 2013 18:25
por young_jedi » Sex Mar 29, 2013 18:25
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Matheus Lacombe O » Sáb Mar 30, 2013 15:08
por Matheus Lacombe O » Sáb Mar 30, 2013 15:08
Olha.. Desde já, obrigado pela resposta.
Mas, seguinte: Eu entendi até a penúltima linha. a partir dali eu continuei diferente.
- Como é:
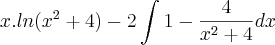
- Não deveria ser:
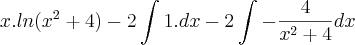
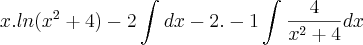

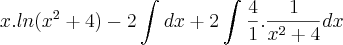
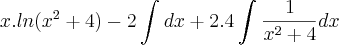

 Resposta:
Resposta: 
- Resposta que não bate com o gabarito :(
Eu não entendi muito bem a passagem da penúltima para a última linha da sua resposta. Se puder esclarecer..

EDIT: E outra.. Por acaso, não tem como resolver usando substituição em "

" logo "de cara" na questão:
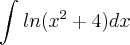
Att. Matheus L. Oliveira
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por young_jedi » Sáb Mar 30, 2013 15:28
por young_jedi » Sáb Mar 30, 2013 15:28
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Matheus Lacombe O » Sáb Mar 30, 2013 16:29
por Matheus Lacombe O » Sáb Mar 30, 2013 16:29
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por young_jedi » Sáb Mar 30, 2013 21:33
por young_jedi » Sáb Mar 30, 2013 21:33
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Qui Dez 22, 2011 17:40
- 1 Respostas
- 3708 Exibições
- Última mensagem por LuizAquino

Qui Dez 22, 2011 21:58
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Sáb Dez 31, 2011 14:35
- 2 Respostas
- 1964 Exibições
- Última mensagem por luiz_henriquear

Sáb Dez 31, 2011 15:08
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Indefinida] Método por Substituição
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- 3 Respostas
- 3009 Exibições
- Última mensagem por e8group

Dom Mar 03, 2013 18:15
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4579 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5621 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
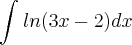
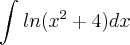
 de K, por exemplo, para poder usar a substituição. Desse jeito eu chamo "u" de "
de K, por exemplo, para poder usar a substituição. Desse jeito eu chamo "u" de " " e "dv" de "
" e "dv" de "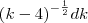 " Mas não dá certo!
" Mas não dá certo! 
![\frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right) \frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right)](/latexrender/pictures/cf4d5c1f673aac5a6b192656d1743349.png)