 por Ge_dutra » Qui Mar 21, 2013 22:51
por Ge_dutra » Qui Mar 21, 2013 22:51
Mostre que arcsen(a) + arcsen(b) = arcsen(a
![\sqrt[]{1-b^2} + b\sqrt[]{1-a^2} \sqrt[]{1-b^2} + b\sqrt[]{1-a^2}](/latexrender/pictures/0cd7cc2e28d07b017c1fface8b99c099.png)
)
Não tenho ideia de como iniciar..
Alguém para ajudar?
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sex Mar 22, 2013 00:19
por e8group » Sex Mar 22, 2013 00:19
Definimos

e
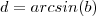
,então

e
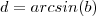
se , e somente se ,
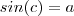
e
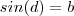
.
Vamos começar desenvolvendo

que é equivalente a

.
Pela identidade trigonométrica fundamental
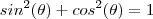
, concluímos
que se
![c,d \in [0,\pi/2] c,d \in [0,\pi/2]](/latexrender/pictures/e36b5c9d23c350e8429bd63dfa4aa0a1.png)
,ou seja , se
![a,b \in [0,1] a,b \in [0,1]](/latexrender/pictures/f3658e9e08765127e56e93a23f7302d3.png)
vale as relações
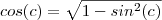
e

. Assim ,
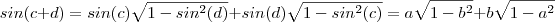
e portanto
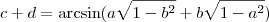
, isto é ,
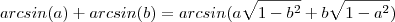
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ge_dutra » Sex Mar 22, 2013 08:56
por Ge_dutra » Sex Mar 22, 2013 08:56
Obrigada!
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- prova da puc
por cleversonluizv » Qui Mar 14, 2013 15:23
- 1 Respostas
- 1378 Exibições
- Última mensagem por young_jedi

Sex Mar 15, 2013 11:36
Análise Combinatória
-
- Prova 1 - 2002
 por admin » Sáb Jul 21, 2007 05:53
por admin » Sáb Jul 21, 2007 05:53
- 0 Respostas
- 1496 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:53
Cálculo Numérico e Aplicações
-
- Prova 1 - 2004
 por admin » Sáb Jul 21, 2007 05:55
por admin » Sáb Jul 21, 2007 05:55
- 0 Respostas
- 1598 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:55
Cálculo Numérico e Aplicações
-
- Prova 2 - 2004
 por admin » Sáb Jul 21, 2007 05:56
por admin » Sáb Jul 21, 2007 05:56
- 0 Respostas
- 1562 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:56
Cálculo Numérico e Aplicações
-
- exercicio de prova 3º ano
por hyenrique » Ter Fev 23, 2010 16:46
- 4 Respostas
- 5596 Exibições
- Última mensagem por hyenrique

Ter Fev 23, 2010 18:22
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{1-b^2} + b\sqrt[]{1-a^2} \sqrt[]{1-b^2} + b\sqrt[]{1-a^2}](/latexrender/pictures/0cd7cc2e28d07b017c1fface8b99c099.png) )
)
 e
e 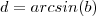 ,então
,então  e
e 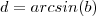 se , e somente se ,
se , e somente se , 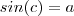 e
e 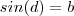 .
. que é equivalente a
que é equivalente a  .
. 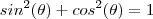 , concluímos
, concluímos![c,d \in [0,\pi/2] c,d \in [0,\pi/2]](/latexrender/pictures/e36b5c9d23c350e8429bd63dfa4aa0a1.png) ,ou seja , se
,ou seja , se ![a,b \in [0,1] a,b \in [0,1]](/latexrender/pictures/f3658e9e08765127e56e93a23f7302d3.png) vale as relações
vale as relações 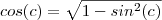 e
e  . Assim ,
. Assim , 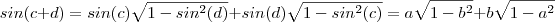 e portanto
e portanto 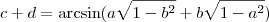 , isto é ,
, isto é , 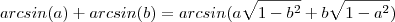



 .
.
 :
: