Estou com um problema na seguinte questão:
Considere a função

1. Ache a equação da reta tangente ao gráfico de f(x) quando
 ;
;2. Calcule a área da região limitada por
 , a reta tangente encontrada no item anterior e o eixo x.
, a reta tangente encontrada no item anterior e o eixo x.------
O item 1 eu resolvi facilmente, pois a definição da reta tangente é
 , onde m é a inclinação da reta tangente (derivada da função).
, onde m é a inclinação da reta tangente (derivada da função).E quando
 a derivada de f é
a derivada de f é 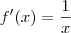
Então a reta tangente é
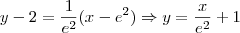
O problema é calcular a área... Não consigo nem imaginar como e onde a curva, a reta e o eixo x se interceptam... Se fosse só a reta e a curva, acho que seria mais fácil... De qualquer forma, quais seriam o intervalos de integração? Se alguém conseguir uma resolução detalhada, eu agradeço.



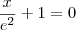



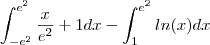

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)