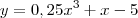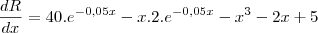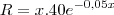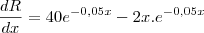por bruno ken taniwaki » Sáb Fev 23, 2013 15:40
por bruno ken taniwaki » Sáb Fev 23, 2013 15:40
Suponha que x unidades de certo produto sejam vendidas quando o preço de cada unidade y é igual a y=40eˆ-0.05 x reais e que o mesmo numero de unidades seja fornecido pelo fabricante quando o preço de cada unidade y é giual a y=0.25xˆ3+x-5 reais
a) Determine a quantidade e o preço de equilibrio
b) Qual é a maxima receita que pode ser obtida?
igualei os dois y
y=y
joguei ln dos dois lados e depois derivei
e deu o resultado
-0.05=3(0.25x)+1/0.25xˆ3+x-5
xˆ3+60xˆ2+4x+60
Essa equacao eu nao consegui resolver, por favor me ajudem
-
bruno ken taniwaki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 23, 2013 15:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administracao
- Andamento: cursando
 por young_jedi » Sáb Fev 23, 2013 20:33
por young_jedi » Sáb Fev 23, 2013 20:33
naão entendi direito as equações, elas são assim

e
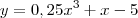
???
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por bruno ken taniwaki » Dom Fev 24, 2013 00:09
por bruno ken taniwaki » Dom Fev 24, 2013 00:09
Sim
-
bruno ken taniwaki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 23, 2013 15:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administracao
- Andamento: cursando
 por young_jedi » Dom Fev 24, 2013 13:26
por young_jedi » Dom Fev 24, 2013 13:26
como y é o preço de cada produto, então o preço total vai ser x.y
para calcular a receita se subtrai o preço de venda pelo de compra


derivando
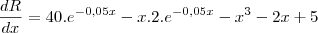
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por bruno ken taniwaki » Dom Fev 24, 2013 14:30
por bruno ken taniwaki » Dom Fev 24, 2013 14:30
Mas e depois disso o que q eu preciso fazer?
-
bruno ken taniwaki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 23, 2013 15:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administracao
- Andamento: cursando
 por bruno ken taniwaki » Dom Fev 24, 2013 14:59
por bruno ken taniwaki » Dom Fev 24, 2013 14:59
Voce nessa questao voce nao fez o lucro e nao a receita
-
bruno ken taniwaki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 23, 2013 15:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administracao
- Andamento: cursando
 por young_jedi » Dom Fev 24, 2013 15:00
por young_jedi » Dom Fev 24, 2013 15:00
voce iguala a derivada a zero e resolve a equação
so que essa equação ai, eu não sei como resolver analiticamente, talvez so por um metodo computacional.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por bruno ken taniwaki » Dom Fev 24, 2013 17:25
por bruno ken taniwaki » Dom Fev 24, 2013 17:25
mas o que voce fez nao foi o lucro?
a Receita nao é somente a primeira parte da equacao?
-
bruno ken taniwaki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Fev 23, 2013 15:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administracao
- Andamento: cursando
 por young_jedi » Dom Fev 24, 2013 18:18
por young_jedi » Dom Fev 24, 2013 18:18
é verdade
a receita é so
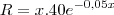
derivando
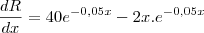

então x=20
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6484 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4523 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2652 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5555 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.