 por klueger » Dom Fev 03, 2013 16:24
por klueger » Dom Fev 03, 2013 16:24
Tenho 3 exercícios trigonométricos para resolver, esqueci como se faz praticamente e se irei usar substituição ou identidade ..
Sei que estou pedindo completa a questão, mas não achei solução aqui.
1)

2)
![\int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx}) \int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx})](/latexrender/pictures/534fec338c45847dbcd65db2773845aa.png)
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Dom Fev 03, 2013 19:00
por e8group » Dom Fev 03, 2013 19:00
Na primeira questão basta tomar

isso por que
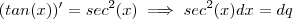
.
Então :
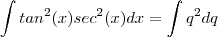
Na segunda questão veja que

(para chegar nesta relação ,multiplicamos a identidade trigonométrica fundamental por
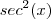
)
Então a questão 2 se resume a
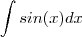
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por klueger » Dom Fev 03, 2013 19:19
por klueger » Dom Fev 03, 2013 19:19
Obrigado.
E quanto a 3? Ali não formatou direito, mas achei a mais complicada
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Dom Fev 03, 2013 19:34
por e8group » Dom Fev 03, 2013 19:34
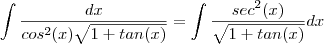
sugiro que faça

. Observe o exercício 1 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8811 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2805 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2437 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2520 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2133 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx}) \int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx})](/latexrender/pictures/534fec338c45847dbcd65db2773845aa.png)


![\int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx}) \int\ (senx+senx.tg^2x.dx)/sec^2x
3) [tex]\int\ dx/(cos^2x .\sqrt{1+tgx})](/latexrender/pictures/534fec338c45847dbcd65db2773845aa.png)

 isso por que
isso por que 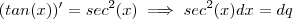 .
. 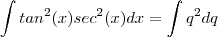
 (para chegar nesta relação ,multiplicamos a identidade trigonométrica fundamental por
(para chegar nesta relação ,multiplicamos a identidade trigonométrica fundamental por 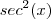 )
)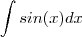


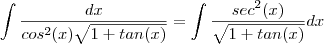
 . Observe o exercício 1 .
. Observe o exercício 1 .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.