 por menino de ouro » Dom Jan 20, 2013 15:31
por menino de ouro » Dom Jan 20, 2013 15:31
Pessoal eu queria uma ajuda para entender como se resolve essas questões para que eu possa sair bem na prova,acho que estou estudando matemática muito mecanicamente, só pelas respostas ou exemplos , sem entendimento. ai quando chega na hora da prova eu agarro!!
1)Esboce a regi ?o e ache a areá da região compreendida entre:
a)os gráficos de f (x) =

b)os graficos de f(x) =

c)os graficos de f(x) =
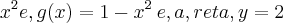
2) esboce o conjunto D e ache a area de D,nos seguintes casos
a) D = ( x,y)


b) D = ( x,y)

R^2 ;

-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por Russman » Dom Jan 20, 2013 20:25
por Russman » Dom Jan 20, 2013 20:25
Vou fazer a 1° de exemplo, você tente fazer as outras e vá expondo suas dúvidas aqui que o ajudaremos.
A primeira coisa interessante a fazer é esboçar os gráficos das funções para VIZUALIZAR a região delimitada por elas, isto é, por suas intersecções.
As funções são

, em verde, e
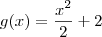
, em vermelho.

- graph
- graph.gif (5.81 KiB) Exibido 4038 vezes
A primeira coisa a fazer é determinar os pontos de intersecção. Para estes temos

, de modo que
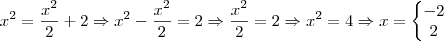
Assim, as funções se intersectam nos pontos

e

Agora, se tomarmos a área entre o eixo

e a função

e subtrairmos da área entre o eixo

e a função

no intervalo
![[-2,2] [-2,2]](/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png)
teremos isolado a região de interesse.
Assim, basta fazer
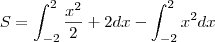
Note que esta região é equivalente a
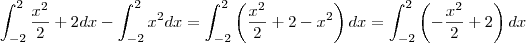
Agora integre, aplique os limites e está feito.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Dom Jan 20, 2013 23:30
por Russman » Dom Jan 20, 2013 23:30
Ele não some. Você faz a operação:

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por menino de ouro » Dom Jan 20, 2013 23:35
por menino de ouro » Dom Jan 20, 2013 23:35
ok,
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por menino de ouro » Dom Jan 20, 2013 23:49
por menino de ouro » Dom Jan 20, 2013 23:49
quando eu tenho duas funções no caso f(x) e g(x) sempre irei igualar para achar os pontos de intercessão? ou não
no caso da letra a) do numero 2 eu só tenho a função y é isso ou não?
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por menino de ouro » Qui Jan 24, 2013 23:34
por menino de ouro » Qui Jan 24, 2013 23:34
como resolvo?
gráfico de

-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral com aplicaçao
 por menino de ouro » Dom Jan 13, 2013 17:11
por menino de ouro » Dom Jan 13, 2013 17:11
- 5 Respostas
- 9391 Exibições
- Última mensagem por Russman

Dom Jan 13, 2013 22:09
Cálculo: Limites, Derivadas e Integrais
-
- Uma aplicação de Integral(ESFERA)
por CuriosoNerde » Dom Mai 31, 2009 20:00
- 1 Respostas
- 3106 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral]Aplicação de fórmula
por Matheus Lacombe O » Sáb Mar 30, 2013 18:25
- 5 Respostas
- 4017 Exibições
- Última mensagem por Russman

Dom Mar 31, 2013 21:19
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL DUPLA - APLICAÇÃO
por sasuyanli » Dom Dez 01, 2013 12:34
- 2 Respostas
- 2294 Exibições
- Última mensagem por sasuyanli

Dom Dez 01, 2013 23:48
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicação de Integral] Área de Revolução
 por carlosce88 » Qua Out 26, 2016 22:40
por carlosce88 » Qua Out 26, 2016 22:40
- 0 Respostas
- 5062 Exibições
- Última mensagem por carlosce88

Qua Out 26, 2016 22:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


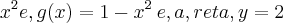


 R^2 ;
R^2 ; 



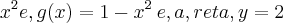


 R^2 ;
R^2 ; 

 , em verde, e
, em verde, e 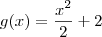 , em vermelho.
, em vermelho. , de modo que
, de modo que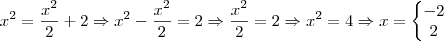
 e
e 
 e a função
e a função  e subtrairmos da área entre o eixo
e subtrairmos da área entre o eixo  e a função
e a função  no intervalo
no intervalo ![[-2,2] [-2,2]](/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png) teremos isolado a região de interesse.
teremos isolado a região de interesse.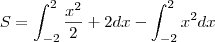
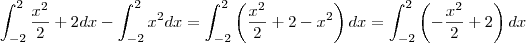

 estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o
estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o 











