Calcule a área plana limitada pelas funções:
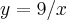 ,
, 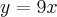 e
e  .
.Achei que seria o seguinte:
Como sabemos, através do estudo deste assunto. Temos que a região será a integral de f(x)-g(x), sendo f(x)>=g(x).
Bem, também sabemos que essa area deve ser subdivida em duas areas menores. A Area total será a soma de S1 e S2.
A minha dúvida é: Eu tenho três funções. Neste caso, a area entre elas será a maior menos as outras? Ou eu subtraio apenas uma?
Me ajudem , please!


 ,
,  e
e  .
.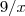 , subtrairia a parte de baixo que é a área do gráfico de
, subtrairia a parte de baixo que é a área do gráfico de  de
de 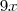 de
de 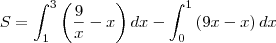


 .
.



