 por menino de ouro » Qui Dez 20, 2012 13:32
por menino de ouro » Qui Dez 20, 2012 13:32
olá,pessoal

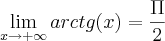
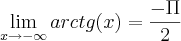
como eu acho esses limites da arctg de(x) e ,também onde eu coloco o resultado la na integral acima para chegar ao resultado de
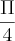
obrigado!
nessa integral aqui

não consigo nem arrancar do inicio!
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por e8group » Sáb Dez 22, 2012 12:19
por e8group » Sáb Dez 22, 2012 12:19
Bom dia , não seria isto abaixo ?
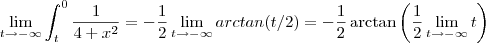
.
Para chegar na resposta ,veja o procedimento .
Dada a função
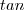
,
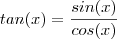
;
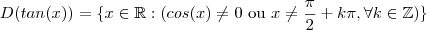
. Mas para obternos a função inversa da tangente vamos precisar trabalhar na imagem e domínio de forma que a função tangente seja injetora e sobrejetora. Assim ,vamos obter que a função tangente possui inversa

. Vamos fazer uma análise de forma obter a resposta do limite .
Temos :
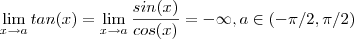
.O fato é que este resultado acima só ocorre quando

para

. Deste modo , temos :

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Dez 22, 2012 14:53
por e8group » Sáb Dez 22, 2012 14:53
Esqueci de postar . Quanto a esta integral

.Vamos dividir em duas etapas .
i)
Temos :
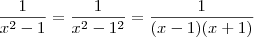
.
Fazendo ,

.
Igualando os coeficientes ,vem :
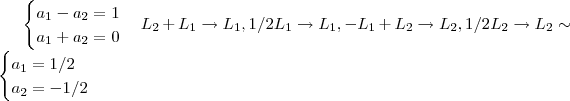
Assim ,

ii)
Rescrevendo a integral inicial como
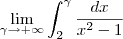
.
Através de (i) e (ii) , segue que :
![\int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right ) \int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right )](/latexrender/pictures/0a45ec7c8858f6622ad486046795e2cf.png)
Consegue terminar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais Impróprias
por menino de ouro » Seg Jan 28, 2013 20:03
- 2 Respostas
- 1535 Exibições
- Última mensagem por menino de ouro

Qua Jan 30, 2013 01:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Impróprias
por menino de ouro » Qui Jan 31, 2013 14:04
- 1 Respostas
- 1270 Exibições
- Última mensagem por e8group

Qui Jan 31, 2013 16:42
Cálculo: Limites, Derivadas e Integrais
-
- Integrais impróprias
por cardoed001 » Dom Jun 08, 2014 17:49
- 2 Respostas
- 2025 Exibições
- Última mensagem por cardoed001

Dom Jun 08, 2014 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integrais Impróprias
por dehcalegari » Qua Out 02, 2013 18:43
- 3 Respostas
- 1809 Exibições
- Última mensagem por dehcalegari

Seg Out 21, 2013 16:36
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8828 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

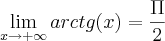
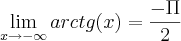
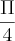
 não consigo nem arrancar do inicio!
não consigo nem arrancar do inicio!

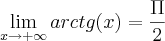
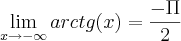
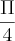
 não consigo nem arrancar do inicio!
não consigo nem arrancar do inicio!
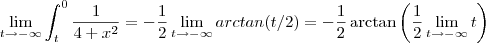 .
. 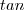 ,
, 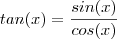 ;
; 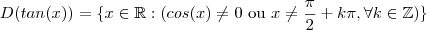 . Mas para obternos a função inversa da tangente vamos precisar trabalhar na imagem e domínio de forma que a função tangente seja injetora e sobrejetora. Assim ,vamos obter que a função tangente possui inversa
. Mas para obternos a função inversa da tangente vamos precisar trabalhar na imagem e domínio de forma que a função tangente seja injetora e sobrejetora. Assim ,vamos obter que a função tangente possui inversa  . Vamos fazer uma análise de forma obter a resposta do limite .
. Vamos fazer uma análise de forma obter a resposta do limite . 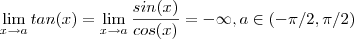 .O fato é que este resultado acima só ocorre quando
.O fato é que este resultado acima só ocorre quando  para
para  . Deste modo , temos :
. Deste modo , temos : 

 .Vamos dividir em duas etapas .
.Vamos dividir em duas etapas .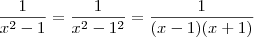 .
.  .
.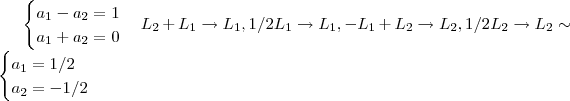

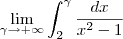 .
. ![\int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right ) \int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right )](/latexrender/pictures/0a45ec7c8858f6622ad486046795e2cf.png)
