 por rodrigonapoleao » Seg Dez 17, 2012 20:39
por rodrigonapoleao » Seg Dez 17, 2012 20:39
Como primitivo por substituição a seguinte função
![f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}} f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}}](/latexrender/pictures/b10a4eef3fb19f071bace0bddf01e34a.png)
?
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Seg Dez 17, 2012 21:38
por e8group » Seg Dez 17, 2012 21:38
Note que ,
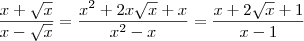
desde que

e

. Como sugestão , faça
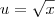
.Comente qual quer coisa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rodrigonapoleao » Seg Dez 17, 2012 22:15
por rodrigonapoleao » Seg Dez 17, 2012 22:15
se
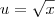
ficaria
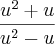
mas como escrevo a derivada de u? preciso de utiliza-la na expressão da primitivação por substituiçao e nao sei como
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Seg Dez 17, 2012 23:22
por e8group » Seg Dez 17, 2012 23:22
Isso mesmo , veja como fica
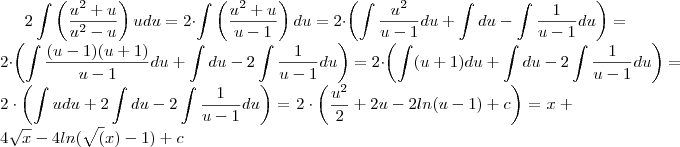
Não sei se ficou didatico , pois omitir algumas contas ,mas qualquer dúvida só postar algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rodrigonapoleao » Ter Dez 18, 2012 10:28
por rodrigonapoleao » Ter Dez 18, 2012 10:28
se u=
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
então u' =
![\frac{1}{2 \sqrt[]{x}} \frac{1}{2 \sqrt[]{x}}](/latexrender/pictures/084b9b16d59d98ee21cb35939806feef.png)
? não estou a entender de onde vem o 2
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Ter Dez 18, 2012 21:58
por e8group » Ter Dez 18, 2012 21:58
Sim , pois
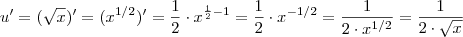
.
Ficou claro ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- primitivaçao por substituiçao
por rodrigonapoleao » Qui Dez 27, 2012 21:04
- 4 Respostas
- 2048 Exibições
- Última mensagem por e8group

Dom Dez 30, 2012 13:32
Cálculo: Limites, Derivadas e Integrais
-
- PRIMITIVAÇÃO
por rodrigonapoleao » Dom Dez 16, 2012 16:49
- 3 Respostas
- 1534 Exibições
- Última mensagem por e8group

Seg Dez 17, 2012 07:26
Cálculo: Limites, Derivadas e Integrais
-
- primitivaçao de funçoes racionais
por rodrigonapoleao » Ter Dez 18, 2012 19:16
- 1 Respostas
- 1319 Exibições
- Última mensagem por e8group

Qua Dez 19, 2012 06:33
Cálculo: Limites, Derivadas e Integrais
-
- Substituição
por LuY12 » Sáb Fev 28, 2009 16:20
- 1 Respostas
- 2041 Exibições
- Última mensagem por Adriano Tavares

Qua Mar 09, 2011 02:37
Cálculo: Limites, Derivadas e Integrais
-
- elasticidade de substituição
por jmario » Ter Mai 25, 2010 10:00
- 1 Respostas
- 2234 Exibições
- Última mensagem por daniellguitar

Sex Jun 04, 2010 00:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}} f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}}](/latexrender/pictures/b10a4eef3fb19f071bace0bddf01e34a.png) ?
?

![f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}} f(x)= \frac{x+\sqrt[]{x}}{x-\sqrt[]{x}}](/latexrender/pictures/b10a4eef3fb19f071bace0bddf01e34a.png) ?
?
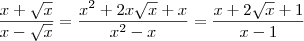 desde que
desde que  e
e  . Como sugestão , faça
. Como sugestão , faça 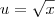 .Comente qual quer coisa .
.Comente qual quer coisa .
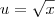 ficaria
ficaria 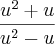

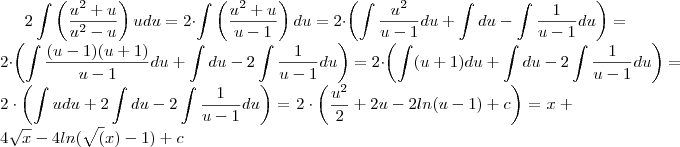

![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) então u' =
então u' = ![\frac{1}{2 \sqrt[]{x}} \frac{1}{2 \sqrt[]{x}}](/latexrender/pictures/084b9b16d59d98ee21cb35939806feef.png) ? não estou a entender de onde vem o 2
? não estou a entender de onde vem o 2
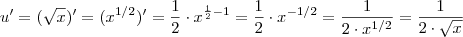 .
. 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
