 uma função qualquer e diferenciável...
uma função qualquer e diferenciável...Como
 , então:
, então: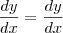
E como
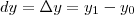
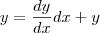 (a grosso modo... pq estou ignorando os índices de
(a grosso modo... pq estou ignorando os índices de  )
)Derivando a igualdade mais uma vez e isolado
 , eu acho que fica assim:
, eu acho que fica assim: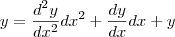
Eu tenho algumas perguntar para fazer com relação a essa manipulação:
i)
 sei que significa
sei que significa 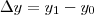 e que
e que 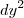 significa
significa 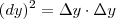 . Ok! Mas que raios esta entidade algébrica,
. Ok! Mas que raios esta entidade algébrica, 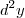 , significa?
, significa?Por exemplo, eu ñ sei isolar o
 em nenhum dos lados da seguinte igualdade,
em nenhum dos lados da seguinte igualdade, 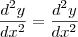 , pq ñ sei o que é esse tal de
, pq ñ sei o que é esse tal de 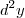 .
.ii) Se é possível isolar o
 nas equações acima, e é, pelo menos é com relação a função linear, então como posso isolar o
nas equações acima, e é, pelo menos é com relação a função linear, então como posso isolar o  em
em 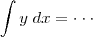 ?
?iii) A pergunta ii) me fez pensar se existe um inverso para o somatório, isto é, um "diferenciatório" ?
Grato!


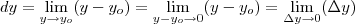 .
.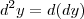 de forma que, como esperado, represente uma variação MUITO pequena( tanto quanto tu queiras) na própria variação MÍNIMA da grandeza
de forma que, como esperado, represente uma variação MUITO pequena( tanto quanto tu queiras) na própria variação MÍNIMA da grandeza  é que quando falamos de formas diferenciais, existe o Lema de Poincaré que diz que
é que quando falamos de formas diferenciais, existe o Lema de Poincaré que diz que 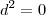 , ou seja, o operador diferencial é nilpotente.
, ou seja, o operador diferencial é nilpotente.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.