 por rhmgh » Sáb Nov 24, 2012 08:19
por rhmgh » Sáb Nov 24, 2012 08:19
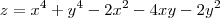
o prof deu esse e alguns outro exercícios para estudar em casa, esse eu estou com dificuldade para fazer porque depois que eu derivo em relação a x e a y faço o sistema e somo as duas equações está dando x = y e ai eu não consigo descobrir a discriminante será que alguém consegue me ajudar?
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Sáb Nov 24, 2012 15:55
por MarceloFantini » Sáb Nov 24, 2012 15:55
Você poderia mostrar suas contas? Não necessariamente está errado, pela sua descrição parece que faltam algumas contas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhmgh » Sáb Nov 24, 2012 23:25
por rhmgh » Sáb Nov 24, 2012 23:25
posso sim, vamos lá
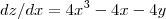
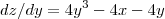
somei as 2, deu:
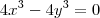

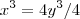
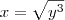
(aqui é raiz cubica ta, eu não consegui fazer o simbolo)
e ai vai ficar:

fazendo as derivadas de segunda ordem:

= A

= C
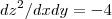
=B
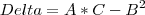
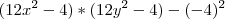
eu travei aqui, não sei como continuar
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Dom Nov 25, 2012 19:30
por MarceloFantini » Dom Nov 25, 2012 19:30
Vamos lá. Primeiro, vamos corrigir sua notação: a que usou significa derivada total, enquanto a correta para derivadas parciais é
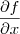
. Então
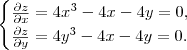
Subtraindo você encontrou que

. Substituindo na primeira equação vem

, logo
![x = y = \sqrt[3]{2} x = y = \sqrt[3]{2}](/latexrender/pictures/2f22e0578a86ac63c5b5c05988bde111.png)
e o par
![(\sqrt[3]{2}, \sqrt[3]{2}) (\sqrt[3]{2}, \sqrt[3]{2})](/latexrender/pictures/435eb55046f25e12f0485013155024d2.png)
talvez seja máximo ou mínimo.
Calculando as derivadas de segunda ordem temos
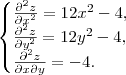
Logo o Hessiano será
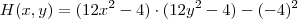
. Substituindo o ponto
![(\sqrt[3]{2}, \sqrt[3]{2}) (\sqrt[3]{2}, \sqrt[3]{2})](/latexrender/pictures/435eb55046f25e12f0485013155024d2.png)
temos que
![H(\sqrt[3]{2}, \sqrt[3]{2}) > 0 H(\sqrt[3]{2}, \sqrt[3]{2}) > 0](/latexrender/pictures/577cc56fe4a1afcfe9a18714299382dd.png)
, portanto um ponto de mínimo local.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhmgh » Ter Nov 27, 2012 08:52
por rhmgh » Ter Nov 27, 2012 08:52
MarceloFantini escreveu: 
não entendi aqui! :S
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Ter Nov 27, 2012 19:09
por MarceloFantini » Ter Nov 27, 2012 19:09
Note que
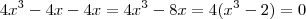
. Eu apenas pulei uma passagem.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhmgh » Ter Nov 27, 2012 23:00
por rhmgh » Ter Nov 27, 2012 23:00
MarceloFantini escreveu:Note que
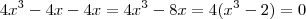
. Eu apenas pulei uma passagem.
ahhhhhh tahh, e também agora que eu percebi que como o x = y você subsituiu ali, não tinha pensado assim ... dããã ... kkk
valeu cara, muito obrigado!

-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Máximo e mínimo
por thadeu » Qua Nov 18, 2009 13:47
- 1 Respostas
- 4168 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 17:50
Trigonometria
-
- [Maximo e Minimo]
por Scheu » Sex Mar 16, 2012 01:23
- 1 Respostas
- 2468 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:14
Cálculo: Limites, Derivadas e Integrais
-
- [Máximo & Minimo]
por allakyhero » Sáb Jun 30, 2012 12:41
- 6 Respostas
- 4916 Exibições
- Última mensagem por allakyhero

Dom Jul 01, 2012 11:06
Cálculo: Limites, Derivadas e Integrais
-
- máximo e minimo
por brunoguim05 » Qua Mai 28, 2014 15:26
- 0 Respostas
- 1550 Exibições
- Última mensagem por brunoguim05

Qua Mai 28, 2014 15:26
Geometria Analítica
-
- Otimização - Máximo e Mínimo
por elbert005 » Dom Jun 05, 2011 20:32
- 0 Respostas
- 4718 Exibições
- Última mensagem por elbert005

Dom Jun 05, 2011 20:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
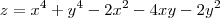




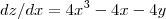
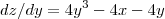
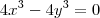

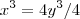
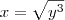 (aqui é raiz cubica ta, eu não consegui fazer o simbolo)
(aqui é raiz cubica ta, eu não consegui fazer o simbolo)
 = A
= A = C
= C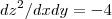 =B
=B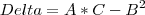
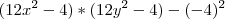
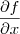 . Então
. Então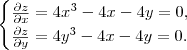
 . Substituindo na primeira equação vem
. Substituindo na primeira equação vem  , logo
, logo ![x = y = \sqrt[3]{2} x = y = \sqrt[3]{2}](/latexrender/pictures/2f22e0578a86ac63c5b5c05988bde111.png) e o par
e o par ![(\sqrt[3]{2}, \sqrt[3]{2}) (\sqrt[3]{2}, \sqrt[3]{2})](/latexrender/pictures/435eb55046f25e12f0485013155024d2.png) talvez seja máximo ou mínimo.
talvez seja máximo ou mínimo. 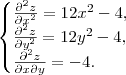
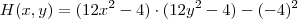 . Substituindo o ponto
. Substituindo o ponto ![H(\sqrt[3]{2}, \sqrt[3]{2}) > 0 H(\sqrt[3]{2}, \sqrt[3]{2}) > 0](/latexrender/pictures/577cc56fe4a1afcfe9a18714299382dd.png) , portanto um ponto de mínimo local.
, portanto um ponto de mínimo local.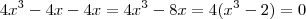 . Eu apenas pulei uma passagem.
. Eu apenas pulei uma passagem.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.