Determine, se a função
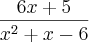 verifica a fórmula
verifica a fórmula![\frac{{(-1)}^{n}n!}{5}\left[ \frac{17}{{(x-2)}^{n+1}}+\frac{13}{{(x+3)}^{n+1}}\right] \frac{{(-1)}^{n}n!}{5}\left[ \frac{17}{{(x-2)}^{n+1}}+\frac{13}{{(x+3)}^{n+1}}\right]](/latexrender/pictures/9544d4e883fb2e45984009e893e9294d.png)
para a sua derivada de ordem n E N.

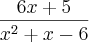 verifica a fórmula
verifica a fórmula![\frac{{(-1)}^{n}n!}{5}\left[ \frac{17}{{(x-2)}^{n+1}}+\frac{13}{{(x+3)}^{n+1}}\right] \frac{{(-1)}^{n}n!}{5}\left[ \frac{17}{{(x-2)}^{n+1}}+\frac{13}{{(x+3)}^{n+1}}\right]](/latexrender/pictures/9544d4e883fb2e45984009e893e9294d.png)


 . Podemos dizer que ,
. Podemos dizer que ,  .
. 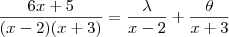 .
.  e
e  que satisfaz a relação acima .
que satisfaz a relação acima .  , vamos obter que :
, vamos obter que : 
 .
. 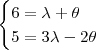
 e
e  .
. 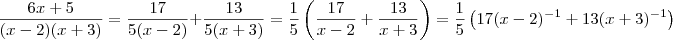
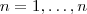 , agora basta desenvolver as derivadas e verificar se condiz com a generalidade proposta e (se vc quiser), mostre que vale para
, agora basta desenvolver as derivadas e verificar se condiz com a generalidade proposta e (se vc quiser), mostre que vale para  .
. 


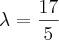 e
e 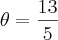 , né?
, né?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.