 por Vidotti » Dom Nov 04, 2012 20:42
por Vidotti » Dom Nov 04, 2012 20:42
-
Vidotti
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 04, 2012 20:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Nov 04, 2012 20:47
por MarceloFantini » Dom Nov 04, 2012 20:47
Note que

, então

. Quando fizer os limites laterais, terá 1 e -1. Além disso, sua resolução das quatro últimas linhas está grosseiramente errada, pois você aplicou o limite e continuou escrevendo-o. Isto é passível de anulamento de nota, pois é erro conceitual.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Vidotti » Dom Nov 04, 2012 21:01
por Vidotti » Dom Nov 04, 2012 21:01
Como eu já disse, fiz apenas 2 aulas, gostaria de saber o por que de estar grosseiramente errado o que fiz nas ultimas linhas.
E a quanto os limites laterais, devo entender que sempre que tiver |x| / x , não existe?
-
Vidotti
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 04, 2012 20:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Nov 04, 2012 21:09
por MarceloFantini » Dom Nov 04, 2012 21:09
Porque sempre após aplicar o limite você deixa de escrevê-lo, por exemplo
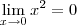
, e não

.
Sim, o limite

não existe. Se tomarmos
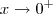
, isto é, aproximando-se da origem pela direita, temos valores positivos para

, daí

e o limite será

. De forma semelhante, tomando
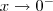
, teremos

e o limite será
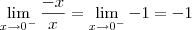
.
Existe um teorema que diz que o limite existe se e somente se os limites laterais são iguais. Como são diferentes o limite não existe.
Editado pela última vez por
MarceloFantini em Seg Nov 05, 2012 10:26, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Vidotti » Dom Nov 04, 2012 21:17
por Vidotti » Dom Nov 04, 2012 21:17
certo, obrigado mesmo pela resposta, era isso mesmo que eu queria saber
-
Vidotti
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Nov 04, 2012 20:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade com limites e módulos
por Luisags » Qui Abr 12, 2012 23:05
- 5 Respostas
- 3843 Exibições
- Última mensagem por gabriel feron

Ter Abr 17, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Dificuldade com raízes
por baloso » Sex Abr 25, 2014 19:22
- 2 Respostas
- 2052 Exibições
- Última mensagem por baloso

Seg Abr 28, 2014 19:33
Cálculo: Limites, Derivadas e Integrais
-
- [Dificuldade] com cálculo de porcentagem
por rkuguyama » Qui Set 18, 2014 13:36
- 1 Respostas
- 4820 Exibições
- Última mensagem por nakagumahissao

Sáb Set 20, 2014 01:03
Probabilidade
-
- ( calculo de volume),tentei fazer mas tenho dificuldade
por vinicastro » Sex Mai 30, 2014 22:54
- 1 Respostas
- 1974 Exibições
- Última mensagem por Russman

Sáb Mai 31, 2014 01:24
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5566 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
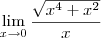

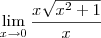


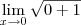

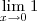

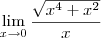

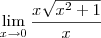


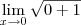

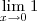

 , então
, então  . Quando fizer os limites laterais, terá 1 e -1. Além disso, sua resolução das quatro últimas linhas está grosseiramente errada, pois você aplicou o limite e continuou escrevendo-o. Isto é passível de anulamento de nota, pois é erro conceitual.
. Quando fizer os limites laterais, terá 1 e -1. Além disso, sua resolução das quatro últimas linhas está grosseiramente errada, pois você aplicou o limite e continuou escrevendo-o. Isto é passível de anulamento de nota, pois é erro conceitual.


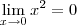 , e não
, e não  .
. não existe. Se tomarmos
não existe. Se tomarmos 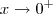 , isto é, aproximando-se da origem pela direita, temos valores positivos para
, isto é, aproximando-se da origem pela direita, temos valores positivos para  , daí
, daí  e o limite será
e o limite será  . De forma semelhante, tomando
. De forma semelhante, tomando 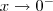 , teremos
, teremos  e o limite será
e o limite será 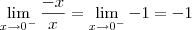 .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.