Então, vou colocar o ex aqui com a minha resolução. Fiz de um jeito e o meu resultado foi 1, porém, na resposta do exercício dá como não existe.
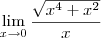

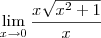


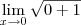

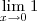

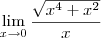

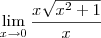


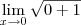

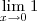

 , então
, então  . Quando fizer os limites laterais, terá 1 e -1. Além disso, sua resolução das quatro últimas linhas está grosseiramente errada, pois você aplicou o limite e continuou escrevendo-o. Isto é passível de anulamento de nota, pois é erro conceitual.
. Quando fizer os limites laterais, terá 1 e -1. Além disso, sua resolução das quatro últimas linhas está grosseiramente errada, pois você aplicou o limite e continuou escrevendo-o. Isto é passível de anulamento de nota, pois é erro conceitual.


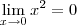 , e não
, e não  .
. não existe. Se tomarmos
não existe. Se tomarmos 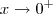 , isto é, aproximando-se da origem pela direita, temos valores positivos para
, isto é, aproximando-se da origem pela direita, temos valores positivos para  , daí
, daí  e o limite será
e o limite será  . De forma semelhante, tomando
. De forma semelhante, tomando 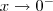 , teremos
, teremos  e o limite será
e o limite será 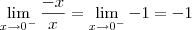 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)