Vamos tomar alguns cuidados.
Sobreira escreveu:O meu questionamento inicial era de que, substituindo o valor para o qual x está tendendo na questão (neste caso 2) de cara é possível verificar que teremos cte/0.

Bom, o que eu gostaria de saber, é se a partir deste instante eu poderia utilizar valores próximos de 2 pela direita (neste caso) para suspeitar o comportamento do infinito se (

ou

).
Resolvendo este:
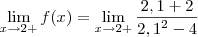
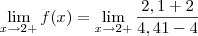
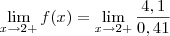
Este resultado nos levaria a suspeitar que se trata de um limite tendendo ao infinito positivo (

)
Primeiro, você está errando grosseiramente a notação ao fazer isto:

. Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.
Sobreira escreveu:E então o professor informou que não aceitaria este procedimento, então por consequência, teríamos que fatorar o denominador para a resolução do exercício (minha dúvida inicial respondida pelo colega MrJuniorFerr neste mesmo tópico).
Como eu disse, resolvi vários exercícios desta forma e as respostas foram corretas e mesmo que com este procedimento, eu esteja "apenas" investigando o comportamento do infinito, gostaria de saber se é válido ou não este procedimento.
O seu professor está correto ao não aceitar este procedimento numa resolução, mas ele está errado quanto à "validade" disto, no sentido em que isso contribui, sim, para entender melhor o comportamento da função. No entanto, como já disse, você
não pode escrever isto numa resolução. Neste exemplo mesmo, a resolução deveria ser algo como:
Escrevendo
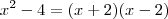
, teremos que o limite torna-se
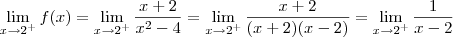
,
onde o denominador irá para zero pela direita, logo positivo, enquanto que o numerador permanece constante, portanto

.
![f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4} f (x) \lim_{4-}\frac{\sqrt[]{16-{x}^{2}}}{x-4}](/latexrender/pictures/ce6d42505c105a7702d299f740a0fa83.png)
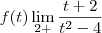


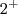 , substituindo 2,01 em t no denominador, você obtém um valor maior que zero, ou seja, o resultado será +infinito.
, substituindo 2,01 em t no denominador, você obtém um valor maior que zero, ou seja, o resultado será +infinito. , o resultado será +infinito. Se c<0 e o denominador tender a
, o resultado será +infinito. Se c<0 e o denominador tender a 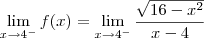 .
. quando na verdade é
quando na verdade é  . Troque uma das duas: escreva
. Troque uma das duas: escreva  ou
ou  .
.

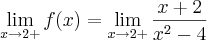

 ou
ou  ).
).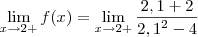
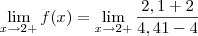
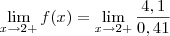
 ).
). . Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.
. Se você 'substituiu' o ponto, por definição não pode escrever o limite junto. Como comentário ao seu método, isto não é uma resolução, porém é válido que você faça tais investigações para entender o comportamento da função. Adotar isto como resposta, no entanto, é errado.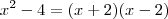 , teremos que o limite torna-se
, teremos que o limite torna-se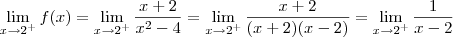 ,
, .
.