 por menino de ouro » Qua Out 24, 2012 23:10
por menino de ouro » Qua Out 24, 2012 23:10
gostaria de aprender a substituir( u.du) nessa questao:
obs: o (e) que multiplica a raiz do lado de fora está elevando o( x ) e o ,(e ) dentro da raiz esta elevando o (-2x)
![\int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx \int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx](/latexrender/pictures/f9b03e4ca99574f1430229e43364c1c4.png)
usando uma dessas formulas dadas:
![\int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a \int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a](/latexrender/pictures/3e4b8a829a8d58b4862603fa6f520676.png)
![\int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a \int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a](/latexrender/pictures/d02a16b28a08e1be2a3a52797edc0676.png)

-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por MarceloFantini » Qui Out 25, 2012 01:27
por MarceloFantini » Qui Out 25, 2012 01:27
Note que
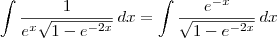
,
e agora faça

, daí
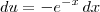
e
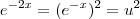
.
Portanto,

.
Agora é só olhar qual é parecida.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1500 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Usando método da substituição
por neoreload » Dom Nov 09, 2014 00:36
- 3 Respostas
- 3855 Exibições
- Última mensagem por e8group

Dom Nov 09, 2014 12:57
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] usando método da substituição
por neoreload » Sex Nov 14, 2014 02:43
- 0 Respostas
- 1558 Exibições
- Última mensagem por neoreload

Sex Nov 14, 2014 02:43
Cálculo: Limites, Derivadas e Integrais
-
- Integração Usando Substituição t = tan Teta/2
por cferreira264 » Dom Jul 02, 2017 19:27
- 0 Respostas
- 1411 Exibições
- Última mensagem por cferreira264

Dom Jul 02, 2017 19:27
Cálculo: Limites, Derivadas e Integrais
-
- [integrais usando substituições indicadas]
por Giu » Sáb Fev 11, 2012 14:08
- 1 Respostas
- 1563 Exibições
- Última mensagem por LuizAquino

Sáb Fev 11, 2012 14:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx \int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx](/latexrender/pictures/f9b03e4ca99574f1430229e43364c1c4.png)
![\int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a \int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a](/latexrender/pictures/3e4b8a829a8d58b4862603fa6f520676.png)
![\int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a \int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a](/latexrender/pictures/d02a16b28a08e1be2a3a52797edc0676.png)


![\int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx \int \frac{1}{e^x \sqrt[]{1-e^-2x}} dx](/latexrender/pictures/f9b03e4ca99574f1430229e43364c1c4.png)
![\int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a \int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a](/latexrender/pictures/3e4b8a829a8d58b4862603fa6f520676.png)
![\int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a \int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a](/latexrender/pictures/d02a16b28a08e1be2a3a52797edc0676.png)


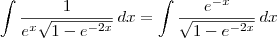 ,
, , daí
, daí 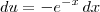 e
e 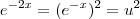 .
. .
.

