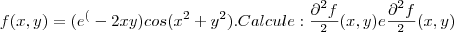
Consegui calcular a derivada primeira em x:
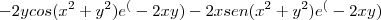
E a derivada primeira em y:
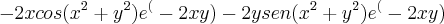
Tenho as respostas das derivadas segundas, mas n´~ao estou conseguindo calculá-las, pois são expressões longas
com vários produtos, não consegui derivar tudo!!
Alguém pode me ajudar?
Derivada segunda em x:
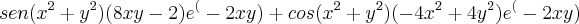
derivada segunda em y:
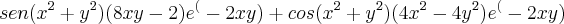


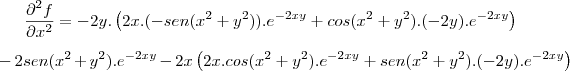
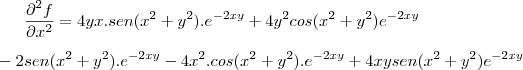
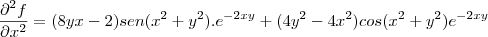

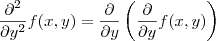
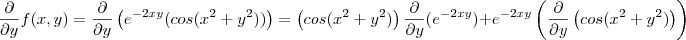
![\frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] . \frac{\partial }{\partial y}f(x,y) = -2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ] .](/latexrender/pictures/a9315b845a009924bf83f392af36d003.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right) \frac{\partial^2 }{\partial y^2}f(x,y) = \frac{\partial }{\partial y}\left(-2e^{-2xy}\left[ ysin(x^2+y^2)+x(cos(x^2+y^2)) \right ]\right)](/latexrender/pictures/62dd5124a8541e81dd372396759baa33.png) .
. 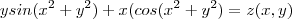 .
. ![\frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2 \frac{\partial }{\partial y}\left(e^{-2xy}\cdot z(x,y) \right) = -2 \left( z(x,y)\left[\frac{\partial }{\partial y}e^{-2xy} \right ] +e^{-2xy}\left[\frac{\partial }{\partial y}z(x,y) \right ]\right )](/latexrender/pictures/11fc44a260833d7ded4ff8f504e74781.png) .
. 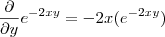 e
e 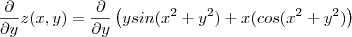
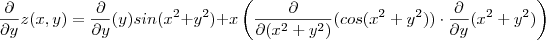
![\frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) \frac{\partial }{\partial y}z(x,y) = sin(x^2+y^2 ) + 2y^2 cos (x^2+y^2) - 2xy sin(x^2+y^2) = sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2)](/latexrender/pictures/73c423bd0b2cec417a5c5f3f4adf6f3d.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) ) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}([-2xysin(x^2+y^2)-2x^2(cos(x^2+y^2)] + sin(x^2 +y^2 )[ 1 -2xy] + 2y^2 cos(x^2+y^2) )](/latexrender/pictures/b1f2dd18d7fc6566248908faac2ab729.png)
![\frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2]) \frac{\partial^2 }{\partial y^2}f(x,y) = -2e^{-2xy}(sin(x^2+y^2)[1-4xy] + cos(x^2+y^2)[2y^2-2x^2])](/latexrender/pictures/8ab03b4f0106d8c26d0dc5b6ce9646c6.png)

![\frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy} \frac{\partial^2 }{\partial y^2}f(x,y) = sin(x^2+y^2)[8xy-2]e^{-2xy} + cos(x^2+y^2)[4x^2-4y^2]e^{-2xy}](/latexrender/pictures/b1303a1fa7262716e522b313109e416d.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)