 por emanes » Qua Out 17, 2012 11:10
por emanes » Qua Out 17, 2012 11:10
Bom dia,
Alguém poderia me ajudar no exercício abaixo, pois estou estudando derivada agora e não estou entendendo o cálculo da taxa de variação:
Um carro A esta indo rumo a oeste a 50km/h e o carro B esta indo rumo norte a 60km/h. Ambos estão se dirigindo para uma encruzilhada das duas retas. A que velocidade os carros estão se aproximando um do outro quando o carro A está a 300m e o carro B está a 400m da encruzilhada?
-
emanes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Ago 17, 2012 09:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: contabil
- Andamento: cursando
 por young_jedi » Qua Out 17, 2012 11:50
por young_jedi » Qua Out 17, 2012 11:50
Podemos notar que um deles faz uma trajetoria vertical e o outro horizontal
vamos dizer que a distancia de A ate a encruzilhada é x e a de B é y
com isso temos que a distancia entre os dois é

em função do tempo

então a velocidade que eles se aproximam é

derivando a equação de s então
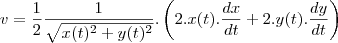
mais voce sabe que
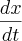
e

, são as velocidades de A e B então substituindo as velocidades e as distancias de A e B chega-se a velocidade e aproximação
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Taxa de variação
por Aliocha Karamazov » Sáb Nov 26, 2011 18:40
- 3 Respostas
- 8063 Exibições
- Última mensagem por MarceloFantini

Dom Nov 27, 2011 01:57
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Taxa de Variação
por Vanny » Dom Set 30, 2012 20:58
- 0 Respostas
- 3111 Exibições
- Última mensagem por Vanny

Dom Set 30, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] - Taxa de Variação
por Jeks_Osodrac » Ter Jul 30, 2013 19:19
- 3 Respostas
- 3269 Exibições
- Última mensagem por Russman

Qua Jul 31, 2013 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada como Taxa de Variação
por Ronaldobb » Sex Set 21, 2012 20:29
- 3 Respostas
- 2265 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 00:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivada taxa de variação - HELP Por favor
por vivik » Ter Mai 15, 2018 16:47
- 0 Respostas
- 2956 Exibições
- Última mensagem por vivik

Ter Mai 15, 2018 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





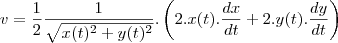
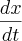 e
e  , são as velocidades de A e B então substituindo as velocidades e as distancias de A e B chega-se a velocidade e aproximação
, são as velocidades de A e B então substituindo as velocidades e as distancias de A e B chega-se a velocidade e aproximação

 .
.



