 por eli83 » Qua Out 10, 2012 10:33
por eli83 » Qua Out 10, 2012 10:33
Aplicando o conceito de exitência de limite, verifique se existe o limite da seguinte função quando x tende para dois:
![f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/4692b09dbdfaaa74cf7c39ffaa8d116d.png)
Fiz utilizando Continuidade.
Se f é contínua em a, então as três condições deverão ser satisfeitas.
existe f(a)
existe
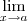
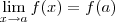
![\lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/75905edffe433a62bc7597ae007d68c6.png)
=
![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png)
(Posso aplicar a definição direta de limite neste caso, pois não terei problemas com o denominador.)
f(2) =
![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png)
E como temos:
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png)
=
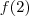
Então existe
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png)
Tenho uma dúvida em relação ao enunciado ele diz aplicando o conceito de existência de limite e eu solucionei aplicando o conceito de continuidade, isto estaria correto.
E também gostaria que verificassem a minha resolução.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por young_jedi » Qua Out 10, 2012 19:27
por young_jedi » Qua Out 10, 2012 19:27
Neste caso voce deve verificar se os limites laterais existem e se são iguais, sendo assim o limite existe
Como o exercicio so pede para verificar a existencia do limite não precisa verificar se a função é continua
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Qua Out 10, 2012 21:06
por MarceloFantini » Qua Out 10, 2012 21:06
Um outro toque, nunca escreva
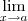
, e sim
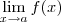
. Só existe limite de funções.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por eli83 » Qui Out 11, 2012 09:16
por eli83 » Qui Out 11, 2012 09:16
E nesse caso como faço. Atribuo valores aleatórios a esquerda e a direita de 2.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por young_jedi » Qui Out 11, 2012 17:25
por young_jedi » Qui Out 11, 2012 17:25
Sim voce atribui valores proximos a 2 pela direita e pela esquerda, veja se eles convergem para um mesmo valor, analisando a questão é possivel ver que sim e portanto o limite existe.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- conceito de integral e limite
por OtavioBonassi » Sex Jan 07, 2011 15:52
- 11 Respostas
- 8692 Exibições
- Última mensagem por OtavioBonassi

Dom Jan 09, 2011 22:47
Cálculo: Limites, Derivadas e Integrais
-
- [verificar a existência] limite trigonométrico
por Fabio Wanderley » Sáb Mar 24, 2012 13:14
- 1 Respostas
- 1487 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 24, 2012 14:49
Cálculo: Limites, Derivadas e Integrais
-
- Existência de limite e se existir, pertence aos reais ou com
por Douglas16 » Qui Fev 28, 2013 20:36
- 3 Respostas
- 2698 Exibições
- Última mensagem por Jhonata

Qui Fev 28, 2013 22:52
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Conceito de Limite
por Raphaela_sf » Qui Abr 05, 2012 19:11
- 3 Respostas
- 2123 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 19:17
Cálculo: Limites, Derivadas e Integrais
-
- Condição de Existência
por gustavowelp » Sáb Jun 26, 2010 11:56
- 5 Respostas
- 5483 Exibições
- Última mensagem por Molina

Sáb Jun 26, 2010 20:49
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} f(x) = {\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/4692b09dbdfaaa74cf7c39ffaa8d116d.png)
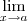
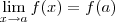
![\lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to a}f(x) = \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/75905edffe433a62bc7597ae007d68c6.png) =
= ![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png) (Posso aplicar a definição direta de limite neste caso, pois não terei problemas com o denominador.)
(Posso aplicar a definição direta de limite neste caso, pois não terei problemas com o denominador.)![{\displaystyle\biggl[24\biggr]^{5}} {\displaystyle\biggl[24\biggr]^{5}}](/latexrender/pictures/ed438677b083c4cdbe4f5513cf245690.png)
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png) =
= 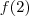
![\lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}} \lim_{x\to 2}{\displaystyle\biggl[\frac{x^3 + 2x +6}{x^2 +5}+ 4 x^2 + 6\biggr]^{5}}](/latexrender/pictures/ee32c0c399d7187fbbcea203bb0cc54c.png)



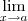 , e sim
, e sim 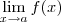 . Só existe limite de funções.
. Só existe limite de funções.

