 por eli83 » Ter Out 09, 2012 11:15
por eli83 » Ter Out 09, 2012 11:15
Encontre o limite da função:
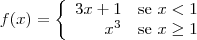
Utilizando limites laterais temos:
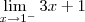
=
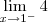
=

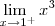
=

O limite de uma existe, em dado ponto, quando existirem os limites laterais (no ponto dado) pela direita e pela esquerda e os mesmos forem iguais.
E neste caso como os limites laterais são diferentes, portanto não existe limite da função no ponto dado.
Gostaria que alguém verificasse se está correta a minha resolução.
Editado pela última vez por
eli83 em Qua Out 10, 2012 00:18, em um total de 1 vez.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por MarceloFantini » Ter Out 09, 2012 18:11
por MarceloFantini » Ter Out 09, 2012 18:11
Novamente, está incorreto o seu uso da notação de limite. Ver a resposta aos tópicos
#1 e
#2.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por eli83 » Ter Out 09, 2012 22:54
por eli83 » Ter Out 09, 2012 22:54
Nossa que vício que é isso. Estou corringo o erro em todos os tópicos.
Grata.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por DanielFerreira » Ter Out 09, 2012 22:59
por DanielFerreira » Ter Out 09, 2012 22:59
Eli83,
que bom vê-la por aqui!
Seja bem-vinda.
Daniel Ferreira.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por eli83 » Qua Out 10, 2012 00:21
por eli83 » Qua Out 10, 2012 00:21
Olá Daniel. Obrigada.
-
eli83
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Out 06, 2012 11:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limite lateral
por Nina » Qua Out 21, 2009 18:25
- 2 Respostas
- 2966 Exibições
- Última mensagem por MarceloFantini

Ter Set 21, 2010 20:18
Cálculo
-
- Limite lateral - dúvida em exercício
por gdf262 » Seg Abr 07, 2014 20:30
- 1 Respostas
- 1618 Exibições
- Última mensagem por Man Utd

Ter Abr 08, 2014 11:56
Cálculo: Limites, Derivadas e Integrais
-
- Area lateral?
por bmachado » Sáb Jun 23, 2012 17:09
- 2 Respostas
- 2525 Exibições
- Última mensagem por bmachado

Dom Jun 24, 2012 12:11
Geometria Espacial
-
- área lateral piramide
 por slade » Dom Out 13, 2013 15:15
por slade » Dom Out 13, 2013 15:15
- 3 Respostas
- 2244 Exibições
- Última mensagem por young_jedi

Ter Out 15, 2013 21:14
Geometria Analítica
-
- [tronco de cone / área lateral] geometrial espacial
por sandra silva » Ter Ago 26, 2008 22:08
- 2 Respostas
- 7121 Exibições
- Última mensagem por sandra silva

Qua Ago 27, 2008 07:34
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
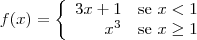
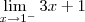 =
= 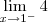 =
= 
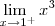 =
= 






 .
.



