Ajuda Matemática • Exibir tópico - integral limitada pelas curvas

Anúncio Global

Respostas

Exibições

Última mensagem

Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25

0 Tópicos

605304 Mensagens

Última mensagem por admin
em Qui Nov 15, 2018 00:25
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58

0 Tópicos

546849 Mensagens

Última mensagem por admin
em Qua Nov 14, 2018 11:58
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51

0 Tópicos

777837 Mensagens

Última mensagem por admin
em Ter Mar 20, 2012 21:51
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04

41 Tópicos

2543450 Mensagens

Última mensagem por Janayna
em Qui Abr 27, 2017 00:04

integral limitada pelas curvas

Regras do fórum

2 mensagens • Página 1 de 1

integral limitada pelas curvas

por ricardosanto » Dom Set 02, 2012 01:11

Enunciado: Calcule usando integral a região limitada pelas curvas.

2)y=9x², y=0 e x=2

eu fiz a 5º da seguinte forma:
5)y=x, y=4x²| <=> 4x²=x <=> 4x²-x=0, daí eu resolvi e encontrei os dois x, q por sua vez, são os limites desta integral ,
e faço as integrais e depois subtraio as áreas.

minha dúvida é: o que devo fazer para encontrar os limites quando a questão possui 3 igualdades?

Muito obrigado pela oportunidade de postar minhas dúvidas

Editado pela última vez por ricardosanto em Dom Set 02, 2012 12:52, em um total de 1 vez.

ricardosanto: Usuário Dedicado; Mensagens: 33; Registrado em: Seg Abr 16, 2012 12:17; Formação Escolar: GRADUAÇÃO; Área/Curso: Engenharia civil; Andamento: cursando

Re: integral limitada pelas curvas

por MarceloFantini » Dom Set 02, 2012 15:31

A reta

x=2

é paralela ao eixo

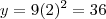. Ela encontra a parábola no ponto y=9 (2)^2 = 36

y=9 (2)^2 = 36

. Portanto você pode fazer $\int_0^2 9 x^2 \, dx$ para calcular a área limitada pela curva.

No outro, os pontos de interseção tem abscissas x = 0

x = 0

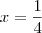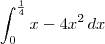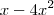e $x= \frac{1}{4}$ , então para calcular a área faça $\int_0^{\frac{1}{4}} x - 4x^2 \, dx$ . A razão de ser x-4x^2

x-4x^2

é que no intervalo [0,1]

[0,1]

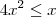temos que $4x^2 \leq x$ , ou seja, a bissetriz dos quadrantes ímpares está acima da parábola.

Futuro MATEMÁTICO
$e^{\pi \cdot i} +1 = 0$

MarceloFantini: Colaborador Moderador; Mensagens: 3126; Registrado em: Seg Dez 14, 2009 11:41; Formação Escolar: GRADUAÇÃO; Andamento: formado

2 mensagens • Página 1 de 1

Voltar para Cálculo: Limites, Derivadas e Integrais

Ir para:

Tópicos relacionados

Respostas

Exibições

Última mensagem

Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02

0 Respostas

1064 Exibições

Última mensagem por Fernandobertolaccini
Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:04

1 Respostas

1414 Exibições

Última mensagem por matmatco
Sáb Ago 09, 2014 12:15
Cálculo: Limites, Derivadas e Integrais
Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58

1 Respostas

1829 Exibições

Última mensagem por LuizAquino
Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
Integral, achar a área da região entre as curvas
por Janoca » Sex Jun 06, 2014 17:24

5 Respostas

4732 Exibições

Última mensagem por alienante
Dom Jun 15, 2014 21:42
Cálculo: Limites, Derivadas e Integrais
Área do triângulo delimitada pelas retas r,s e t
por flaaacs » Qua Out 03, 2012 16:02

3 Respostas

2932 Exibições

Última mensagem por young_jedi
Qua Out 03, 2012 17:25
Geometria Analítica

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

Assunto: Princípio da Indução Finita
Autor: Fontelles - Dom Jan 17, 2010 14:42

Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?
$2n \geq n+1 ,\forall n \in\aleph*$
O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois $2.1 \geq 1+1$
2°) Admitamos que $P(k), k \in \aleph*$ , seja verdadeira:
$2k \geq k+1$ (hipótese da indução)
e provemos que $2(k+1) \geq (K+1)+1$
Temos: (Nessa parte)
$2(k+1) = 2k+2 \geq (k+1)+2 > (k+1)+1$

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Seg Jan 18, 2010 01:55

Boa noite Fontelles.

Não sei se você está familiarizado com o Princípio da Indução Finita, portanto vou tentar explicar aqui.

Ele dá uma equação, no caso:

$2n \geq n+1, \forall n \in \aleph^{*}$

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

$2*1 \geq 1+1$

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para k+1

k+1

.

$\mbox{Suponhamos que P(k), }k \in \aleph^{*},\mbox{ seja verdadeiro:}$
$2k \geq k+1$

$\mbox{Vamos provar que:}$
$2(k+1) \geq (k+1)+1$

Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.

Espero ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Fontelles - Seg Jan 18, 2010 02:28

Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!

Assunto: Princípio da Indução Finita
Autor: Fontelles - Qui Jan 21, 2010 11:32

Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Jan 21, 2010 12:25

Boa tarde Fontelles!

Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.

O que temos que provar é isso: $2(k+1) \geq (k+1)+1$ , certo? O autor começou do primeiro membro:

2(k+1)= 2k+2

2(k+1)= 2k+2

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

$2k+2 \geq (k+1)+2$

Que é outra verdade. Agora, com certeza:

(k+1)+2 > (k+1)+1

(k+1)+2 > (k+1)+1

Agora, como 2(k+1)

2(k+1)

é $\geq$ a (k+1)+2

(k+1)+2

, e este por sua vez é sempre

que

(k+1)+1

, logo:

$2(k+1) \geq (k+1)+1 \quad \mbox{(c.q.d)}$

Inclusive, nunca é igual, sempre maior.

Espero (dessa vez) ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Caeros - Dom Out 31, 2010 10:39

Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?

Assunto: Princípio da Indução Finita
Autor: andrefahl - Dom Out 31, 2010 11:37

c.q.d. = como queriamos demonstrar =)

Assunto: Princípio da Indução Finita
Autor: Abelardo - Qui Mai 05, 2011 17:33

Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Mai 05, 2011 20:05

Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Assunto: Princípio da Indução Finita
Autor: Vennom - Qui Abr 26, 2012 23:04

MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa. :-D

:-D

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.