 por e8group » Dom Jun 17, 2012 14:37
por e8group » Dom Jun 17, 2012 14:37
Limites no "infinito " prova a existência de pelo menos uma raiz real ?
Considerando uma função polinomial (continua para todos reais) f definida por
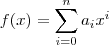
, de forma que

,

converge para

e

. Isto prova a existência de pelo menos uma raiz real ? se não ,qual seria o método ?
Obrigado !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Jun 19, 2012 01:34
por MarceloFantini » Ter Jun 19, 2012 01:34
Evite dizer que

converge para mais ou menos infinito, diga que tende a mais ou menos infinito. Como polinômios são funções contínuas, pelo teorema do valor intermediário existe algum ponto onde ele se anula. É isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Ter Jun 19, 2012 11:20
por e8group » Ter Jun 19, 2012 11:20
MarceloFantini escreveu:Evite dizer que converge para mais ou menos infinito, diga que tende a mais ou menos infinito. Como polinômios são funções contínuas, pelo teorema do valor intermediário existe algum ponto onde ele se anula. É isso.
OK ! Agradeço pela atenção . Fazendo uma analogia entre as assíntotas verticais e horizontais , O que significa

e
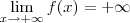
? Pergunto isso porque não vi ainda uma explicação para este comportamento ?
OBS .: Eu tenho um exercício de uma lista de limites que pede para mostra que todo polinômio de maior grau impar tem pelo menos uma raiz real (dica : ver limites no infinito ). Peço desculpas pelo erro da notação .abraços .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Limite de Raiz "m" de "infinito"
por antonelli2006 » Sáb Set 17, 2011 05:56
- 5 Respostas
- 9178 Exibições
- Última mensagem por LuizAquino

Dom Set 18, 2011 10:08
Cálculo: Limites, Derivadas e Integrais
-
- Limites, quando podem resultar em "Infinito"?
por rafa_0910 » Dom Nov 02, 2014 14:17
- 3 Respostas
- 2799 Exibições
- Última mensagem por Russman

Seg Nov 03, 2014 02:23
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida Limite no infinito "m<n"
por elyjunior » Seg Set 26, 2011 22:59
- 2 Respostas
- 1816 Exibições
- Última mensagem por LuizAquino

Ter Set 27, 2011 17:09
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Problema na "prova" das regras operatórias
por Subject Delta » Qua Abr 25, 2012 17:37
- 2 Respostas
- 2820 Exibições
- Última mensagem por Subject Delta

Qua Abr 25, 2012 21:23
Cálculo: Limites, Derivadas e Integrais
-
- Sistemas Lineares: "a, b e c" como "soluções".
por allendy » Qua Set 08, 2010 20:28
- 2 Respostas
- 11298 Exibições
- Última mensagem por allendy

Qua Set 08, 2010 20:37
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
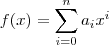 , de forma que
, de forma que  ,
,  converge para
converge para  e
e  . Isto prova a existência de pelo menos uma raiz real ? se não ,qual seria o método ?
. Isto prova a existência de pelo menos uma raiz real ? se não ,qual seria o método ?
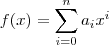 , de forma que
, de forma que  ,
,  converge para
converge para  e
e  . Isto prova a existência de pelo menos uma raiz real ? se não ,qual seria o método ?
. Isto prova a existência de pelo menos uma raiz real ? se não ,qual seria o método ?
 converge para mais ou menos infinito, diga que tende a mais ou menos infinito. Como polinômios são funções contínuas, pelo teorema do valor intermediário existe algum ponto onde ele se anula. É isso.
converge para mais ou menos infinito, diga que tende a mais ou menos infinito. Como polinômios são funções contínuas, pelo teorema do valor intermediário existe algum ponto onde ele se anula. É isso.

 e
e 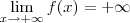 ? Pergunto isso porque não vi ainda uma explicação para este comportamento ?
? Pergunto isso porque não vi ainda uma explicação para este comportamento ? 