 por rhmgh » Dom Jun 10, 2012 14:53
por rhmgh » Dom Jun 10, 2012 14:53
Bom Dia
Meu Profº passou uma lista de exericios e eu fiquei na duvida na resolução de alguns tem como alguém me ajudar?
os exercicios são
y= x² . (Raiz Quadrada de 9 - 4x²) --- o 9-4x² está tudo dentro da raiz
y= ( x³ - 1) . Raiz Cubica de 1 + 3x --- o 1 + 3x está tudo dentro da raiz
y = (x² - 1) (1 - 2x) (1 - 3x²)
y = cos³ (x/3)
Atc
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Jhonata » Dom Jun 10, 2012 15:31
por Jhonata » Dom Jun 10, 2012 15:31
Para esses exercícios(e pra toda sua vida diante do cálculo), é fundamental que estude a regra do produto, a regra do quociente e a regra da cadeia, mas basicamente, são dadas pelas fórmulas abaixo, respectivamente:
Se f(x) e g(x) são diferenciáveis.

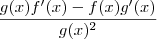
Se y for diferenciável em x e f(x) for derivável em g(x).
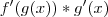
Se tiver alguma dúvida relacionado a isso, pergunte... Se eu puder ajudar, ficarei feliz.
.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por rhmgh » Dom Jun 10, 2012 22:51
por rhmgh » Dom Jun 10, 2012 22:51
assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Jhonata » Dom Jun 10, 2012 22:55
por Jhonata » Dom Jun 10, 2012 22:55
rhmgh escreveu:assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
Bem, isso você pega com o tempo e claro que tem que ter muita dedicação, portanto, estude.
Você não deve deixar as "letras" amedrontarem você. Seria bom você ver alguns exemplos, prestar atenção neles(por exemplo, os passos até a resposta final) e se possível, tentar refazê-los, utilizar a base que você tem pra seguir adiante também é fundamental...
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por rhmgh » Dom Jun 10, 2012 22:58
por rhmgh » Dom Jun 10, 2012 22:58
Jhonata escreveu:rhmgh escreveu:assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
Bem, isso você pega com o tempo e claro que tem que ter muita dedicação, portanto, estude.
Você não deve deixar as "letras" amedrontarem você. Seria bom você ver alguns exemplos, prestar atenção neles(por exemplo, os passos até a resposta final) e se possível, tentar refazê-los, utilizar a base que você tem pra seguir adiante também é fundamental...
você sabe onde eu posso encontrar varios desses exemplos?
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Jhonata » Dom Jun 10, 2012 23:01
por Jhonata » Dom Jun 10, 2012 23:01
Jhonata escreveu:rhmgh escreveu:assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
Bem, isso você pega com o tempo e claro que tem que ter muita dedicação, portanto, estude.
Você não deve deixar as "letras" amedrontarem você. Seria bom você ver alguns exemplos, prestar atenção neles(por exemplo, os passos até a resposta final) e se possível, tentar refazê-los, utilizar a base que você tem pra seguir adiante também é fundamental...
Veja só, essa função que você pegou: y= x² . (Raiz Quadrada de 9 - 4x²), pra facilitar, vamos escrever assim:
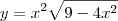
, observe que nesse caso, há uma multiplicação entre as funções:

e

, então utilizaremos a regra do produto(verifique as relações que postei antes).
Nesse caso, chamamos
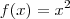
e
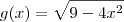
. Tente agora aplicar a fórmula e veja o que consegue.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Dom Jun 10, 2012 23:05
por Jhonata » Dom Jun 10, 2012 23:05
rhmgh escreveu:Jhonata escreveu:rhmgh escreveu:assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
Bem, isso você pega com o tempo e claro que tem que ter muita dedicação, portanto, estude.
Você não deve deixar as "letras" amedrontarem você. Seria bom você ver alguns exemplos, prestar atenção neles(por exemplo, os passos até a resposta final) e se possível, tentar refazê-los, utilizar a base que você tem pra seguir adiante também é fundamental...
você sabe onde eu posso encontrar varios desses exemplos?
Acho que uma ótima solução, seria estudar com as video aulas que o amigo postou acima, mas segue o link do canal das video aulas pra cálculo I:
http://www.youtube.com/playlist?list=PL ... ature=plcpou
http://www.youtube.com/playlist?list=PL ... ature=plcpUtilizo esses videos como "material" de estudo e me ajudam bastante.
Recomendo o acompanhamento desses videos por um livro, sugiro o James Steward 6a edição, mas na internet você dificilmente encontrará pra baixar, mas encontrará facilmente a 5a edição. O livro contém muitos exemplos com muitas resoluções detalhadas.

" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por rhmgh » Dom Jun 10, 2012 23:10
por rhmgh » Dom Jun 10, 2012 23:10
Jhonata escreveu:rhmgh escreveu:Jhonata escreveu:rhmgh escreveu:assisti o video, tenho a tabelinha também, as regras...
mais a minha dificuldade ainda é encaixar os numeros no lugar das letras, eu ainda não to conseguindo identificar o que é o que, não peguei o jeito ainda...alguém tem alguma dica?
Bem, isso você pega com o tempo e claro que tem que ter muita dedicação, portanto, estude.
Você não deve deixar as "letras" amedrontarem você. Seria bom você ver alguns exemplos, prestar atenção neles(por exemplo, os passos até a resposta final) e se possível, tentar refazê-los, utilizar a base que você tem pra seguir adiante também é fundamental...
você sabe onde eu posso encontrar varios desses exemplos?
Acho que uma ótima solução, seria estudar com as video aulas que o amigo postou acima, mas segue o link do canal das video aulas pra cálculo I:
http://www.youtube.com/playlist?list=PL ... ature=plcpou
http://www.youtube.com/playlist?list=PL ... ature=plcpUtilizo esses videos como "material" de estudo e me ajudam bastante.
Recomendo o acompanhamento desses videos por um livro, sugiro o James Steward 6a edição, mas na internet você dificilmente encontrará pra baixar, mas encontrará facilmente a 5a edição. O livro contém muitos exemplos com muitas resoluções detalhadas.

Bele, muito obrigado pela força...vo dar uma intensivada ver se eu pego o jeito, encontrei o livro para download 5ª Edição!
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12555 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada
por alienpuke » Sáb Out 24, 2015 15:45
- 2 Respostas
- 6984 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2015 16:12
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada
por beel » Dom Set 25, 2011 13:04
- 2 Respostas
- 6888 Exibições
- Última mensagem por beel

Dom Set 25, 2011 16:22
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada de log
por beel » Sáb Out 15, 2011 22:42
- 4 Respostas
- 7453 Exibições
- Última mensagem por beel

Ter Out 18, 2011 13:16
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada de log 2
por beel » Dom Out 16, 2011 01:10
- 2 Respostas
- 6435 Exibições
- Última mensagem por Fabio Cabral

Ter Out 18, 2011 13:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




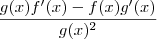
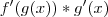

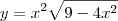 , observe que nesse caso, há uma multiplicação entre as funções:
, observe que nesse caso, há uma multiplicação entre as funções:  e
e  , então utilizaremos a regra do produto(verifique as relações que postei antes).
, então utilizaremos a regra do produto(verifique as relações que postei antes).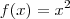 e
e 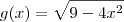 . Tente agora aplicar a fórmula e veja o que consegue.
. Tente agora aplicar a fórmula e veja o que consegue.


 , avisa que eu resolvo.
, avisa que eu resolvo.

