Suponha que a diminuição na pressão sanguínea de uma pessoa dependa de uma determinada droga que ela deverá tomar. Assim, se x mg da droga forem tomados, a queda na pressão sanguínea será uma função de x. Seja f(x) esta função:
f (x) = 1/2 x² (k - x)
onde x está em [0, k] e k é uma constante positiva; Determine o valor de x que cause o maior decréscimo na pressão sanguínea.
Resolução:
Para resolver este problema, sei que o ponto máximo da função deve ser encontrado, para isso devemos derivar essa função e depois igualar à zero.
Mas não estou conseguindo fazer a derivada!




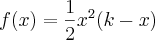

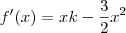
 ou
ou 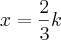 .
.
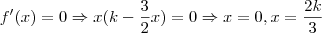 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)