ricardosanto escreveu:Ola, desejo que alguém analise estas resoluções, para eu saber se estou respondendo certo.
As suas soluções estão corretas.
ricardosanto escreveu:resolvi de acordo com exemplos que vi no livro, e nao sei pq ele não usa o método dos dois caminhos para a resolução.
Porque nesse caso é como se você já tivesse provado, usando todas aquelas considerações sobre os caminhos, que
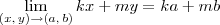
.
Em seguida, você está apenas simplificando todos os limites apresentados para que fiquem nesse formato básico.
ricardosanto escreveu:Se estas respostas estiverem corretas, eu posso afirmar que o limite eh este numero que encontrei? (zero, dois e menos um)
Sim.
ricardosanto escreveu:O que a negaçao (
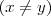
na A e B e

na C ) pode afetar na resolução?
Essas restrições (ou condições de existência) servem para que os limites fiquem bem definidos. No itens A) e B), note que não poderia haver x = y, pois apareceria uma divisão por zero. Já no item c), a divisão por zero apareceria caso x = 1.
Tipicamente, essas restrições não precisam ser ditas de forma explícita no exercício. A pessoa deve ser capaz de olhar para a função dentro do limite e reconhecer essas restrições. Nesse contexto, o método de resolução que você empregou não é afetado por isso.
![\lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex] \lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex]](/latexrender/pictures/4cd2443b58e27bd81b521cddbc0ef07c.png)


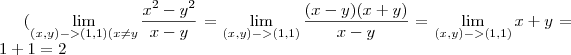




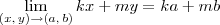 .
. na A e B e
na A e B e  na C ) pode afetar na resolução?
na C ) pode afetar na resolução?


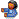
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.