O gradiente de uma função determina a máxima taxa de variação certo?
O vetor mostra a direção e o modulo (que poderia ser chamado de "intensidade"?) dessa variação.. certo?
e a taxa mínima? como encontrar?



vinik1 escreveu:O gradiente de uma função determina a máxima taxa de variação certo?
O vetor mostra a direção e o modulo (que poderia ser chamado de "intensidade"?) dessa variação.. certo?
e a taxa mínima? como encontrar?
 indica a direção e o sentido da maior variação, sendo que
indica a direção e o sentido da maior variação, sendo que 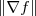 é o valor (a intensidade) dessa maior variação.
é o valor (a intensidade) dessa maior variação. indica a direção e o sentido da menor variação, sendo que
indica a direção e o sentido da menor variação, sendo que  é o valor (a intensidade) dessa menor variação.
é o valor (a intensidade) dessa menor variação.

vinik1 escreveu:Certo...
A minha duvida era, se alterar o sinal, o modulo permanece o mesmo, entao a "intensidade" prevalece.
logo essa taxa na variação nao seria mínima, seria máxima em modulo, porem negativa.
Era isso que nao conseguia entender, mas de qualquer forma minha duvida foi resolvida. Muito obrigado.
 , que é representada por
, que é representada por 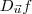 , é dada por:
, é dada por:
 é o ângulo formado entre os vetores
é o ângulo formado entre os vetores  e
e  , então temos que:
, então temos que: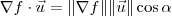
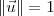 (já que o vetor é unitário), temos que:
(já que o vetor é unitário), temos que:
 é 1, enquanto que o mínimo é -1.
é 1, enquanto que o mínimo é -1.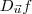 assume é
assume é 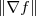 , enquanto que o mínimo é
, enquanto que o mínimo é  .
.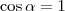 , precisamos de
, precisamos de  . Ou seja, para que
. Ou seja, para que 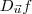 seja máxima, os vetores
seja máxima, os vetores  e
e  devem possuir a mesma direção e sentido.
devem possuir a mesma direção e sentido. , precisamos de
, precisamos de  . Ou seja, para que
. Ou seja, para que 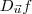 seja mínima, os vetores
seja mínima, os vetores  e
e  devem possuir a mesma direção e sentidos contrários.
devem possuir a mesma direção e sentidos contrários. , enquanto que a menor variação ocorre na direção e sentido dados por
, enquanto que a menor variação ocorre na direção e sentido dados por  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

