Gostaria de ajuda na seguinte questão, que envolve derivadas com uso da regra do produto, regra da cadeia e trigonometria. Resolvi a questão em uma apostila, mas a solução está diferente do meu resultado e eu gostaria de verificar com vocês. Posto abaixo minha resolução e a resposta dada.
Determinar a derivada da expressão abaixo
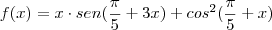
Resolvi da seguinte forma:
 (derivada da soma = soma das derivadas)
(derivada da soma = soma das derivadas)Na primeira derivada, como é um produto, aplico a regra do produto. Na segunda, aplico a regra da cadeia. Sendo assim, temos:
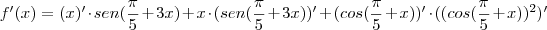

Então, minha resposta ficou assim:

E a resposta da apostila é a seguinte:

Eu estou errado ou a resposta que está errada?
Desde já, muito obrigado pela ajuda de vocês!


 . Note que:
. Note que:![\left[\textrm{sen}\,\left(\frac{\pi}{5}+3x\right)\right]^\prime = \left[\cos \left(\frac{\pi}{5}+3x\right)\right]\left(\frac{\pi}{5}+3x\right)^\prime = 3\cos \left(\frac{\pi}{5}+3x\right) \left[\textrm{sen}\,\left(\frac{\pi}{5}+3x\right)\right]^\prime = \left[\cos \left(\frac{\pi}{5}+3x\right)\right]\left(\frac{\pi}{5}+3x\right)^\prime = 3\cos \left(\frac{\pi}{5}+3x\right)](/latexrender/pictures/7e3e36ec5a8e98ae84038c03d9adfac4.png)
 temos que aplicar a regra da cadeia duas vezes. Note que:
temos que aplicar a regra da cadeia duas vezes. Note que:![\left\{\left[\cos \left(\frac {\pi}{5}+x\right)\right]^2\right\}^\prime = 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[\cos\left(\frac {\pi}{5}+x\right)\right]^\prime \left\{\left[\cos \left(\frac {\pi}{5}+x\right)\right]^2\right\}^\prime = 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[\cos\left(\frac {\pi}{5}+x\right)\right]^\prime](/latexrender/pictures/f0cdd24c89d8dc14338505ea1d34cbb5.png)
![= 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[-\,\textrm{sen}\,\left(\frac {\pi}{5}+x\right)\right]\left[\left(\frac {\pi}{5}+x\right)\right]^\prime = 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[-\,\textrm{sen}\,\left(\frac {\pi}{5}+x\right)\right]\left[\left(\frac {\pi}{5}+x\right)\right]^\prime](/latexrender/pictures/d0c906817d07581dbb53ae32743b62e6.png)
![= 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[-\,\textrm{sen}\,\left(\frac {\pi}{5}+x\right)\right]\cdot 1 = 2\left[\cos \left(\frac {\pi}{5}+x\right)\right]\left[-\,\textrm{sen}\,\left(\frac {\pi}{5}+x\right)\right]\cdot 1](/latexrender/pictures/6069ead502523ea009097435043bf34a.png)
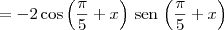
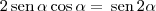 , temos que:
, temos que:


 .
.
 :
: