 por cjunior94 » Dom Mar 25, 2012 22:54
por cjunior94 » Dom Mar 25, 2012 22:54
Estou resolvendo alguns exercícios sobre limites trigonométricos e me deparei com uma questão que não consegui resolver:

No local onde encontrei esse exercício avia uma resolução, mas não consegui entender ela completamente:


![\lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]} \lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]}](/latexrender/pictures/3f2f4fc398a372cc58275fbae109a921.png)
Sendo:
![sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)] sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)]](/latexrender/pictures/c720d5a3da75240c7d87fab88bebd33e.png)
Consegui perceber que ocorreu uma multiplicação por

na fracão e também que foi colocado o -1 em evidencia, mas não consegui entender a afirmação que:
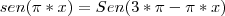
Editado pela última vez por
cjunior94 em Seg Mar 26, 2012 01:07, em um total de 1 vez.
-
cjunior94
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 18, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Wanderley » Seg Mar 26, 2012 00:55
por Fabio Wanderley » Seg Mar 26, 2012 00:55
cjunior94 escreveu:![sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)] sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)]](/latexrender/pictures/c720d5a3da75240c7d87fab88bebd33e.png)
Consegui perceber que ocorreu uma multiplicação por

na fracão e também que foi colocado o -1 em evidencia, mas não consegui entender a afirmação que:
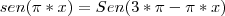
Foi usada a relação sen(a - b) = sen(a).cos(b) - sen(b).cos(a).
Mas como terminou a resolução desse limite?
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por cjunior94 » Seg Mar 26, 2012 01:12
por cjunior94 » Seg Mar 26, 2012 01:12
Mesmo após você falar que foi usada a formula de diferença de senos eu não consegui identificar o que foi realmente feito. Pode me explicar detalhadamente?
Logo após:
![\lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]} \lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]}](/latexrender/pictures/3f2f4fc398a372cc58275fbae109a921.png)
já foi colocada a resposta :
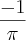
-
cjunior94
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 18, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Mar 26, 2012 01:21
por LuizAquino » Seg Mar 26, 2012 01:21
cjunior94 escreveu:Mesmo após você falar que foi usada a formula de diferença de senos eu não consegui identificar o que foi realmente feito. Pode me explicar detalhadamente?
Aplique a fórmula do seno da diferença:
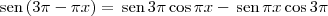
Agora responda as perguntas abaixo.
1) Qual é o valor de

?
2) Qual é o valor de
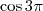
?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite trigonometrico indeterminado
por ewald » Qui Mai 26, 2011 15:15
- 11 Respostas
- 5836 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 02:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado
por ewald » Qui Mai 05, 2011 17:55
- 1 Respostas
- 1847 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado 0/0
por ewald » Qui Mai 05, 2011 19:08
- 1 Respostas
- 4361 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 19:41
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado
por ewald » Ter Mai 17, 2011 15:40
- 13 Respostas
- 6641 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 18, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado ? - ?
por cjunior94 » Ter Mai 01, 2012 22:00
- 1 Respostas
- 1871 Exibições
- Última mensagem por LuizAquino

Qua Mai 02, 2012 14:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]} \lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]}](/latexrender/pictures/3f2f4fc398a372cc58275fbae109a921.png)
![sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)] sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)]](/latexrender/pictures/c720d5a3da75240c7d87fab88bebd33e.png)
 na fracão e também que foi colocado o -1 em evidencia, mas não consegui entender a afirmação que:
na fracão e também que foi colocado o -1 em evidencia, mas não consegui entender a afirmação que: 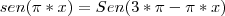



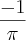
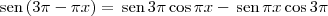
 ?
?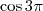 ?
?


 , avisa que eu resolvo.
, avisa que eu resolvo.

