 por Ademir Jose » Sex Mar 09, 2012 21:45
por Ademir Jose » Sex Mar 09, 2012 21:45
Lim x-> 2

Eu fui resolvendo o limite e achei as raízes (x-3).(x +1/2) para o divisor, sendo que na resposta aparece (x-3).(2x +1). Alguém poderia me explicar detalhadamente como isso acontece ?
-
Ademir Jose
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 09, 2012 21:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por ant_dii » Sáb Mar 10, 2012 01:55
por ant_dii » Sáb Mar 10, 2012 01:55
Como você disse, você encontrou as raízes de

, isso significa fazer
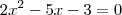
, de onde temos

Veja que isto significa o mesmo que
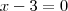
ou
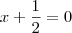
.
Desta última, podemos fazer a seguinte dedução lógica
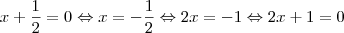
Portanto,
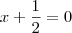
é o mesmo que

.
Entendeu???
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por LuizAquino » Sáb Mar 10, 2012 09:00
por LuizAquino » Sáb Mar 10, 2012 09:00
Ademir Jose escreveu:
Eu fui resolvendo o limite e achei as raízes (x-3).(x +1/2) para o divisor, sendo que na resposta aparece (x-3).(2x +1).
ant_dii escreveu:Como você disse, você encontrou as raízes de

, isso significa fazer 2x^2 - 5x - 3=0, de onde temos

Vocês dois cometeram um erro muito comum: esquecer do coeficiente que multiplica o termo

.
O correto é:
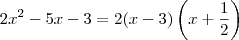
Arrumando o produto que aparece no segundo membro, podemos escrever que:
![2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right] 2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right]](/latexrender/pictures/5e154778188960f49a64e9b06f2c937c.png)

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por joaofonseca » Sáb Mar 10, 2012 11:42
por joaofonseca » Sáb Mar 10, 2012 11:42
Existe uma técnica de fatorização, para quando o coeficiente do termo quadrádico é maior que 1.Em inglês chamam-lhe o "bottom-up".
E funciona assim:
1)Multiplica-se o coficiente do termo quadratico pelo termo independente.Neste caso temos 2x(-3)=-6.
2)Agora a tipica pergunta: quais os dois números cujo poduto é -6 e a soma é -5.Sabemos de antemão que os dois números terão sinais diferentes e o maior será negativo.Fica:

(a solução 2 e -3 ou 3 e -2 não daria resultado, porque apesar do produto ser -6 a soma não seria -5)
Esta expressão ainda não é equivalente à inicial dáda.
Agora temos de dividir os termos independentes por 2, que é o coeficiente do termo quadrático.Se resultar em divisão não inteira o denominador passa como coeficiente do termo em
x:


Na pratica é o que o LuizAquino já disse, mas de uma forma mais automática.Nem é preciso pensar muito!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Mar 10, 2012 13:41
por LuizAquino » Sáb Mar 10, 2012 13:41
joaofonseca escreveu:Na pratica é o que o LuizAquino já disse, mas de uma forma mais automática.Nem é preciso pensar muito!
Isso é que causa problema: "não pensar".
"Decorar" os conteúdos de Matemática e executá-los de uma forma "automática" (sem "pensar muito"), tipicamente gera uma grande quantidade de erros!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Ademir Jose » Dom Mar 11, 2012 19:14
por Ademir Jose » Dom Mar 11, 2012 19:14
Gente, muito obrigado! Obrigado mesmo!
-
Ademir Jose
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 09, 2012 21:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Limites com duas raízes
por Atom » Dom Mai 25, 2014 20:22
- 1 Respostas
- 2059 Exibições
- Última mensagem por e8group

Dom Mai 25, 2014 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25709 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
-
- Limites com Raízes Cúbicas
por nathilopes » Qua Mar 05, 2014 02:23
- 2 Respostas
- 2908 Exibições
- Última mensagem por nathilopes

Qua Mar 05, 2014 16:09
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Dificuldade com raízes
por baloso » Sex Abr 25, 2014 19:22
- 2 Respostas
- 2044 Exibições
- Última mensagem por baloso

Seg Abr 28, 2014 19:33
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda, Limites com Raizes
por rodrigojuara » Ter Mar 10, 2015 22:39
- 1 Respostas
- 1177 Exibições
- Última mensagem por adauto martins

Qua Mar 11, 2015 13:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 , isso significa fazer
, isso significa fazer 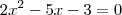 , de onde temos
, de onde temos 
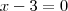 ou
ou 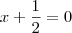 .
.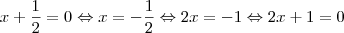
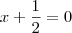 é o mesmo que
é o mesmo que  .
.
, isso significa fazer 2x^2 - 5x - 3=0, de onde temos
 .
. 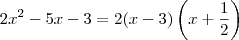
![2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right] 2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right]](/latexrender/pictures/5e154778188960f49a64e9b06f2c937c.png)













