 por Keleber » Sex Fev 03, 2012 16:05
por Keleber » Sex Fev 03, 2012 16:05
Eu gostaria de saber como se precessa uma derivada de varios produtos: Como esta:
(f(x)g(x)H(x)L(x))´.
Por exemplo: qual a derivada de:
x²x³x. ou também, já que é de praxe usar senos e cosenos: (sen(x)cos(x)tang(x))´ e outras mais que puderem exemplificar.
-
Keleber
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 14:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sex Fev 03, 2012 21:37
por LuizAquino » Sex Fev 03, 2012 21:37
Keleber escreveu:Eu gostaria de saber como se processa uma derivada de vários produtos: Como esta:
(f(x)g(x)H(x)L(x))´.
Basta ir agrupando em duas partes e aplicando a derivada do produto. Desse modo, você pode obter a relação desejada.
![[f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime [f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime](/latexrender/pictures/fbf824199dcd1acfb6963dd9b6fc1fd5.png)
![=[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)] =[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)]](/latexrender/pictures/a9034c05257b995eb3afd829c3aeab2a.png)
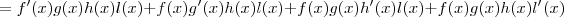
Keleber escreveu:Por exemplo: qual a derivada de:
x²x³x. ou também, já que é de praxe usar senos e cosenos: (sen(x)cos(x)tang(x))´ e outras mais que puderem exemplificar.
Tente aplicar a ideia que ilustrei acima.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ant_dii » Sex Fev 03, 2012 21:42
por ant_dii » Sex Fev 03, 2012 21:42
Vamos estudar o caso de três funções, depois você poderá estender.
Supondo todas contínuas e deriváveis, vamos considerar que a multiplicação de duas funções é ainda uma função, ou seja, que
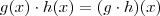
.
Agora, (preste atenção aos passos) temos
![(f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh' (f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh'](/latexrender/pictures/6efa23362c756b902c93ed729beba150.png)
Apartir daí é possível generalizar...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por ant_dii » Sex Fev 03, 2012 21:43
por ant_dii » Sex Fev 03, 2012 21:43
Mil desculpas Luiz, não vi que já havia respondido...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por LuizAquino » Sex Fev 03, 2012 21:49
por LuizAquino » Sex Fev 03, 2012 21:49
ant_dii escreveu:Mil desculpas Luiz, não vi que já havia respondido...
Sem problema!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Keleber » Sáb Fev 04, 2012 11:29
por Keleber » Sáb Fev 04, 2012 11:29
Muito bom todas as respostas e exemplificações.
Eu vou tentar generalizar para equações do tipo: (x²2x/x³x²)´. Acredito que o método seja o mesmo. Também, generalizar para outros operadores seja bastante útil.
Como por exemplo: operadores cujo o produto não seja o produto dos operadores.
Obrigado e até a próxima.
-
Keleber
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 14:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7467 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4938 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2963 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1990 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![[f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime [f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime](/latexrender/pictures/fbf824199dcd1acfb6963dd9b6fc1fd5.png)
![=[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)] =[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)]](/latexrender/pictures/a9034c05257b995eb3afd829c3aeab2a.png)
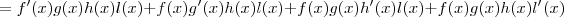

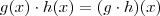 .
.![(f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh' (f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh'](/latexrender/pictures/6efa23362c756b902c93ed729beba150.png)



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.