Não sei se foi erro de digitação, mas na hora de estudar limites, derivadas e integrais, cuide muito do sinal, pois ele pode trazer complicações...
Digo isso como dica, pois você escreveu assim
Profeta escreveu:Resp:
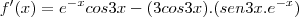
Mas, o limite deve ser calculado da seguinte forma:
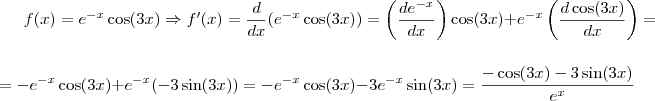
É só uma dica, já que você está tão empenhado e não desejo que desista ou se sinta frustado diante de um resultado que nunca bate...
Só os loucos sabem...
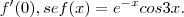
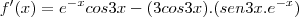



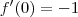



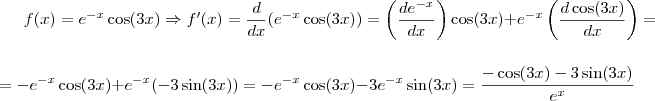


 .
.
 :
: